Gaussian Process Classification

Exact inference in Gaussian process models with likelihood functions tailored to classification isn't tractable. Here we consider two procedures for approximate inference for binary classification:

Laplace's approximation is based on an expansion around the mode of the posterior:
1. a description of the implementation of the algorithm
2. a simple example applying the algorithm to a 2-dimensional classification problem
3. a somewhat more involved example, classifying images of hand-written digits.
The Expectation Propagation (EP) algorithm is based on matching moments approximations to the marginals of the posterior:
1. a description of the implementation of the algorithm
2. a simple example applying the algorithm to a 2-dimensional classification problem
3. a somewhat more involved example, classifying images of hand-written digits.

The code, demonstration scripts and documentation are all contained in the tar or zip archive file.

Laplace's Approximation

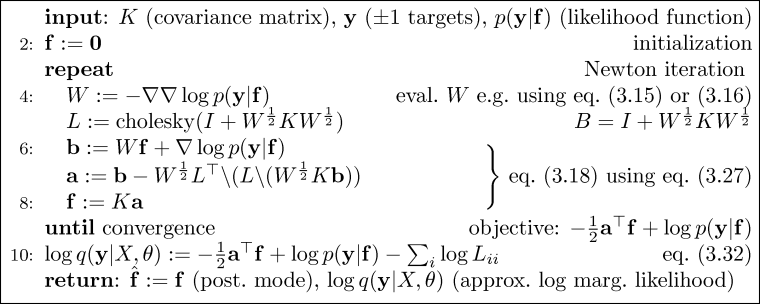
It is straight forward to implement Laplace's method for binary Gaussian process classification using matlab. Here we discuss an implementation which relies closely on Algorithm 3.1 (p. 46) for computing Laplace's approximation to the posterior, Algorithm 3.2 (p. 47) for making probabilistic predictions for test cases and Algorithm 5.1 (p. 126) for computing partial derivatives of the log marginal likelihood w.r.t. the hyperparameters (the parameters of the covariance function). Be aware that the negative of the log marginal likelihood is used.

The implementation given in binaryLaplaceGP.m can conveniently be used together with minimize.m. The program can do one of two things:

compute the negative log marginal likelihood and its partial derivatives wrt. the hyperparameters, usage
```
[nlml dnlml] = binaryLaplaceGP(logtheta, covfunc, lik, x, y)
```
which is used when "training" the hyperparameters, or

compute the (marginal) predictive distribution of test inputs, usage

[p mu s2 nlml] = binaryLaplaceGP(logtheta, covfunc, lik, x, y, xstar)

Selection between the two modes is indicated by the presence (or absence) of test cases, xstar. The arguments to the binaryLaplaceGP.m function are given in the table below where n is the number of training cases, D is the dimension of the input space and nn is the number of test cases:

inputs
`logtheta`	a (column) vector containing the logarithm of the hyperparameters
`covfunc`	the covariance function, see covFunctions.m
`lik`	the likelihood function, built-in functions are: `logistic` and `cumGauss`.
`x`	a `n` by `D` matrix of training inputs
`y`	a (column) vector (of length `n`) of training set `+1/-1` binary targets
`xstar`	(optional) a `nn` by `D` matrix of test inputs

outputs
`nlml`	the negative log marginal likelihood
`dnlml`	(column) vector with the partial derivatives of the negative log marginal likelihood wrt. the logarithm of the hyperparameters.
`mu`	(column) vector (of length `nn`) of predictive latent means
`s2`	(column) vector (of length `nn`) of predictive latent variances
`p`	(column) vector (of length `nn`) of predictive probabilities

The number of hyperparameters (and thus the length of the logtheta vector) depends on the choice of covariance function. Below we will used the squared exponential covariance function with isotropic distance measure, implemented in covSEiso.m; this covariance function has 2 parameters.

Properties of various covariance functions are discussed in section 4.2. For the details of the implementation of the above covariance functions, see covFunctions.m and the two likelihood functions logistic and cumGauss are placed at the end of the binaryLaplaceGP.m file. In either mode (training or testing) the program first uses Newton's algorithm to find the maximum of the posterior over latent variables. In the first ever call of the function, the initial guess for the latent variables is the zero vector. If the function is called multiple times, it stores the optimum from the previous call in a persistent variable and attempts to use this value as a starting guess for Newton's algorithm. This is useful when training, e.g. using minimize.m, since the hyperparameters for consecutive calls will generally be similar, and one would expect the maximum over latent variables based on the previous setting of the hyperparameters as a reasonable starting guess. (If it turns out that this strategy leads to a very bad marginal likelihood value, then the function reverts to starting at zero.)

The Newton algorithm follows Algorithm 3.1, section 3.4, page 46

The iterations are terminated when the improvement in log marginal likelihood drops below a small tolerance. During the iterations, it is checked that the log marginal likelihood never decreases; if this happens bisection is repeatedly applied (up to a maximum of 10 times) until the likelihood increases.

What happens next depends on whether we are in the training or prediction mode, as indicated by the absence or presence of test inputs xstar. If test cases are present, then predictions are computed following Algorithm 3.2, section 3.4, page 47

Alternatively, if we are in the training mode, we proceed to compute the partial derivatives of the log marginal likelihood wrt the hyperparameters, using Algorithm 5.1, section 5.5.1, page 126

Example of Laplace's Approximation applied to a 2-dimensional classification problem

You can either follow the example below or run the short demo_laplace_2d.m script. First we generate a simple artificial classification dataset, by sampling data points from each of two classes from separate Gaussian distributions, as follows:

  n1=80; n2=40;                         % number of data points from each class
  S1 = eye(2); S2 = [1 0.95; 0.95 1];             % the two covariance matrices
  m1 = [0.75; 0]; m2 = [-0.75; 0];                              % the two means

  randn('seed',17)
  x1 = chol(S1)'*randn(2,n1)+repmat(m1,1,n1);          % samples from one class
  x2 = chol(S2)'*randn(2,n2)+repmat(m2,1,n2);              % and from the other

  x = [x1 x2]';                                      % these are the inputs and
  y = [repmat(-1,1,n1) repmat(1,1,n2)]';         % outputs used a training data

Below the samples are show together with the "Bayes Decision Probabilities", obtained from complete knowledge of the data generating process:

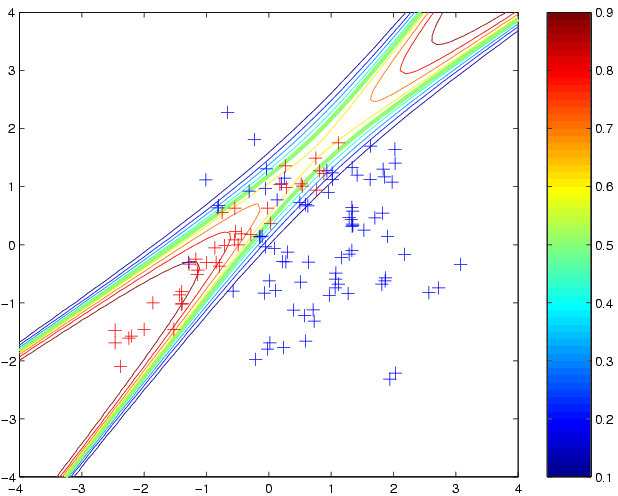
Note, that the ideal predictive probabilities depend only on the relative density of the two classes, and not on the absolute density. We would, for example, expect that the structure in the upper right hand corner of the plot may be very difficult to obtain based on the samples, because the data density is very low. The contour plot is obtained by:

  [t1 t2] = meshgrid(-4:0.1:4,-4:0.1:4);
  t = [t1(:) t2(:)];                                % these are the test inputs

  tt = sum((t-repmat(m1',length(t),1))*inv(S1).*(t-repmat(m1',length(t),1)),2);
  z1 = n1*exp(-tt/2)/sqrt(det(S1));
  tt = sum((t-repmat(m2',length(t),1))*inv(S2).*(t-repmat(m2',length(t),1)),2);
  z2 = n2*exp(-tt/2)/sqrt(det(S2));

  contour(t1,t2,reshape(z2./(z1+z2),size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

Now, we will fit a probabilistic Gaussian process classifier to this data, using an implementation of Laplace's method. We must specify a covariance function and a likelihood function. First, we will try the squared exponential covariance function covSEiso. We must specify the parameters of the covariance function (hyperparameters). For the isotropic squared exponential covariance function there are two hyperparameters, the lengthscale (kernel width) and the magnitude. We need to specify values for these hyperparameters (see below for how to learn them). Initially, we will simply set the log of these hyperparameters to zero, and see what happens. For the likelihood function, we use the cumulative Gaussian:

  loghyper = [0; 0];
  p2 = binaryLaplaceGP(loghyper, 'covSEiso', 'cumGauss', x, y, t);
  clf
  contour(t1,t2,reshape(p2,size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

to produce predictive probabilities on the grid of test points:

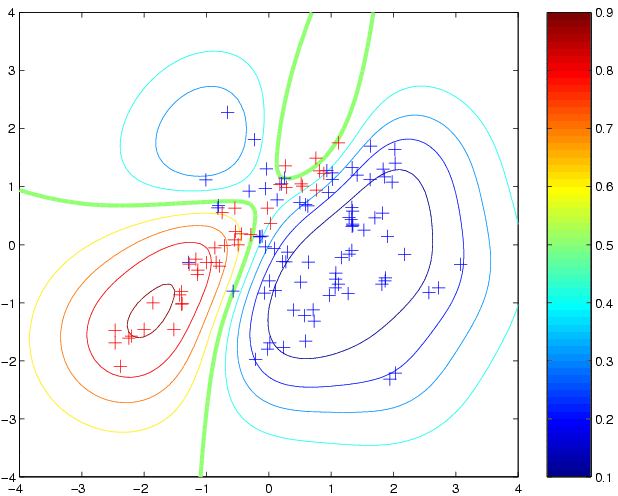
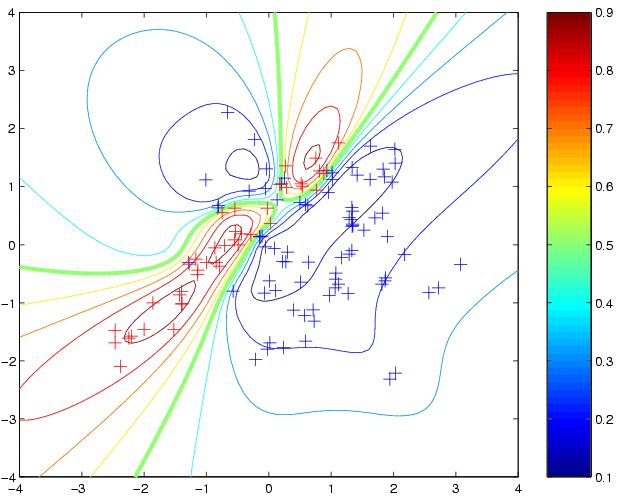
Although the predictive contours in this plot look quite different from the "Bayes Decision Probabilities" plotted above, note that the predictive probabilities in regions of high data density are not terribly different from those of the generating process. Recall, that this plot was made using hyperparameter which we essentially pulled out of thin air. Now, we find the values of the hyperparameters which maximize the marginal likelihood (or strictly, the Laplace approximation of the marginal likelihood):

  newloghyper = minimize(loghyper, 'binaryLaplaceGP', -20, 'covSEiso', 'cumGauss', x, y)
  p3 = binaryLaplaceGP(newloghyper, 'covSEiso', 'cumGauss', x, y, t);

where the argument -20 tells minimize to evaluate the function at most 20 times. The new hyperparameters have a fairly similar length scale, but a much larger magnitude for the latent function. This leads to more extreme predictive probabilities:

  clf
  contour(t1,t2,reshape(p3,size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

produces:

Note, that this plot still shows that the predictive probabilities revert to one half, when we move away from the data (in stark contrast to the "Bayes Decision Probabilities" in this example). This may or may not be seen as an appropriate behaviour, depending on our prior expectations about the data. It is a direct consequence of the behaviour of the squared exponential covariance function. We can instead try a neural network covariance function covNNiso.m, which has the ability to saturate at specific latent values, as we move away from zero:

  newloghyper = minimize(loghyper, 'binaryLaplaceGP',-20,'covNNiso','cumGauss',x,y);
  p4 = binaryLaplaceGP(newloghyper, 'covNNiso','cumGauss', x, y, t);
  clf
  contour(t1,t2,reshape(p4,size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

to produce:

which shows a somewhat less pronounced tendency for the predictive probabilities to tend to one half as we move towards the boundaries of the plot.

Example of Laplace's Approximation applied to hand-written digit classification

You can either follow the example below or run the short demo_laplace_usps.m script. You will need the code form the tar or zip archive and additionally the data, see below. Consider compiling the mex files (see README file), although the programs should work even without.

As an example application we will consider the USPS resampled data which can be found here. Specifically, we will need to download usps_resampled.mat and unpack the data from bz2 (7.0 Mb) or zip (8.3 Mb) files. As an example, we will consider the binary classification task of separating images of the digit "3" from images of the digit "5".

  [x y xx yy] = loadBinaryUSPS(3,5);

which will create the training inputs x (of size 767 by 256), binary (+1/-1) training targets y (of length 767), and xx and yy containing the test set (of size 773). Use e.g. imagesc(reshape(x(3,:),16,16)'); to view an image (here the 3rd image of the training set).

Now, let us make predictions using the squared exponential covariance function covSEiso and the cumulative Gaussian likelihood function cumGauss. We must specify the parameters of the covariance function (hyperparameters). For the isotropic squared exponential covariance function there are two hyperparameters, the characteristic length-scale (kernel width) and the signal magnitude. We need to specify values for these hyperparameters (see below for how to learn them). One strategy, which is perhaps not too unreasonable would be to set the characteristic length-scale to be equal to the average pair-wise distance between points, which for this data is around 22; the signal variance can be set to unity, since this is the range at which the sigmoid non-linearity comes into play. Other strategies for setting initial guesses for the hyperparameters may be reasonable as well. We need to specify the logarithm of the hypers, roughly log(22)=3 and log(1)=0:

  loghyper = [3.0; 0.0];   % set the log hyperparameters
  p = binaryLaplaceGP(loghyper, 'covSEiso', 'cumGauss', x, y, xx);

which may take a few seconds to compute. We can visualize the predictive test set probabilities using:

  plot(p,'.')
  hold on
  plot([1 length(p)],[0.5 0.5],'r')

to get:

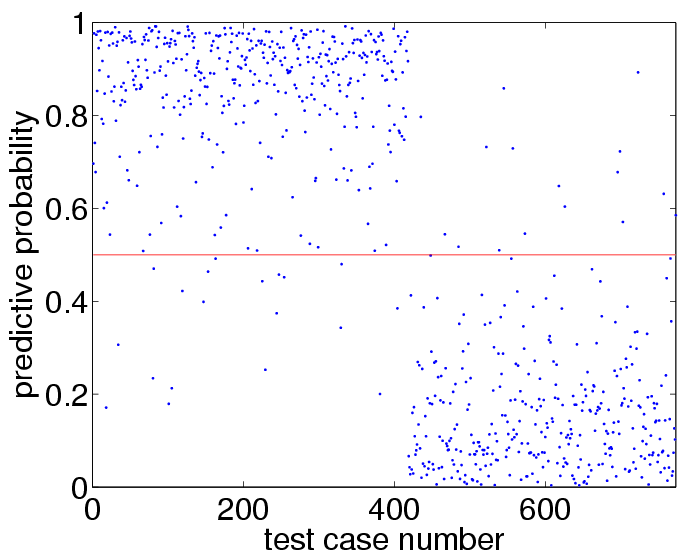
where we should keep in mind that the test cases are ordered according to their target class. Notice that there are misclassifications, but there are no very confident misclassifications. The number of test set errors (out of 773 test cases) when thresholding the predictive probability at 0.5 and the average amount of information about the test set labels in excess of a 50/50 model in bits are given by:

  sum((p>0.5)~=(yy>0))
  mean((yy==1).*log2(p)+(yy==-1).*log2(1-p))+1

which shows test set 35 prediction errors (out of 773 test cases) and an average amount of information of about 0.71 bits, compare to Figure 3.7(b) and 3.7(d) on page 64.

More interestingly, we can also use the program to find the values for the hyperparameters which optimize the marginal likelihood, as follows:

  [loghyper' binaryLaplaceGP(loghyper, 'covSEiso', 'cumGauss', x, y)]
  [newloghyper logmarglik] = minimize(loghyper, 'binaryLaplaceGP', -20, 'covSEiso', 'cumGauss', x, y);
  [newloghyper' logmarglik(end)]

where the third argument -20 to the minimize function, tells minimize to evaluate the function at most 20 times (this is adequate when the parameter space is only 2-dimensional. Above, we first evaluate the negative log marginal likelihood at our initial guess for loghyper (which is about 222), then minimize the negative log marginal likelihood w.r.t. the hyperparameters, to obtain new values of 2.75 for the log lengthscale and 2.27 for the log magnitude. The negative log marginal likelihood decreases to about 99 at the minimum, see also Figure 3.7(a) page 64. The marginal likelihood has thus increased by a factor of exp(222-99) or roughly 3e+53.

Finally, we can make test set predictions with the new hyperparameters:

  pp = binaryLaplaceGP(newloghyper, 'covSEiso', 'cumGauss', x, y, xx);
  plot(pp,'g.')

to obtain:

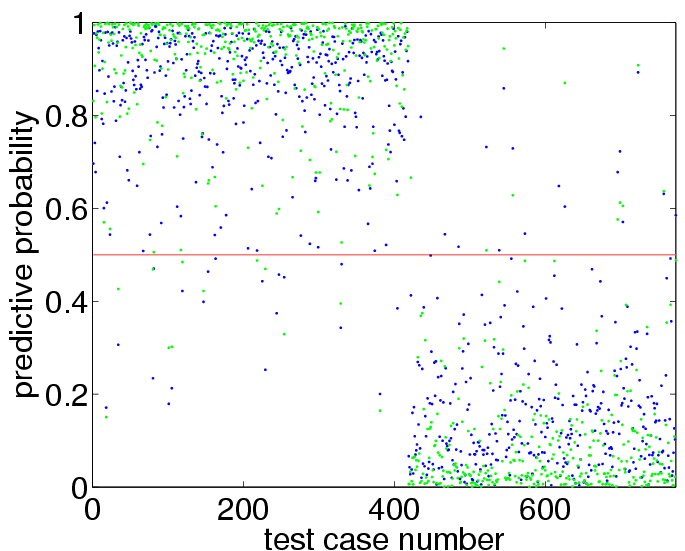
We note that the new predictions (in green) generally take more extreme values than the old ones (in blue). Evaluating the new test predictions:

  sum((pp>0.5)~=(yy>0))
  mean((yy==1).*log2(pp)+(yy==-1).*log2(1-pp))+1

reveals that there are now 22 test set misclassifications (as opposed to 35) and the information about the test set labels has increased from 0.71 bits to 0.83 bits.

2. The Expectation Propagation Algorithm

It is straight forward to implement the Expectation Propagation (EP) algorithm for binary Gaussian process classification using matlab. Here we discuss an implementation which relies closely on Algorithm 3.5 (p. 58) for computing the EP approximation to the posterior, Algorithm 3.6 (p. 59) for making probabilistic predictions for test cases and Algorithm 5.2 (p. 127) for computing partial derivatives of the log marginal likelihood w.r.t. the hyperparameters (the parameters of the covariance function). Be aware that the negative of the log marginal likelihood is used.

The implementation given in binaryEPGP.m can conveniently be used together with minimize.m. The program can do one of two things:

compute the negative log marginal likelihood and its partial derivatives wrt. the hyperparameters, usage
```
[nlml dnlml] = binaryEPGP(logtheta, covfunc, x, y)
```
which is used when "training" the hyperparameters, or
compute the (marginal) predictive distribution of test inputs, usage
```
[p mu s2 nlml] = binaryEPGP(logtheta, cov, x, y, xstar)
```

Selection between the two modes is indicated by the presence (or absence) of test cases, xstar. The arguments to the binaryEPGP.m function are given in the table below where n is the number of training cases, D is the dimension of the input space and nn is the number of test cases:

inputs
`logtheta`	a (column) vector containing the logarithm of the hyperparameters
`covfunc`	the covariance function, see covFunctions.m
`x`	a `n` by `D` matrix of training inputs
`y`	a (column) vector (of length `n`) of training set `+1/-1` binary targets
`xstar`	(optional) a `nn` by `D` matrix of test inputs

outputs
`nlml`	the negative log marginal likelihood
`dnlml`	(column) vector with the partial derivatives of the negative log marginal likelihood wrt. the logarithm of the hyperparameters.
`mu`	(column) vector (of length `nn`) of predictive latent means
`s2`	(column) vector (of length `nn`) of predictive latent variances
`p`	(column) vector (of length `nn`) of predictive probabilities

The number of hyperparameters (and thus the length of the logtheta vector) depends on the choice of covariance function. Below we will use the squared exponential covariance functions with isotropic distance measure, implemented in covSEiso.m: this covariance function has 2 parameters.

Properties of various covariance functions are discussed in section 4.2. For the details of the implementation of the above covariance functions, see covFunctions.m. In either mode (training or testing) the program first uses sweeps of EP updates to each latent variable in turn. Every update recomputes new values for the tilde parameters ttau and tnu (and updates the parameters of the posterior mu and Sigma. In the first ever call of the function, the initial guess for the tilde parameters ttau and tnu are both the zero vector. If the function is called multiple times, it stores the optimum from the previous call in a persistent variable and attempts to use these values as a starting guess for subsequent EP updates. This is useful when training, e.g. using minimize.m, since the hyperparameters for consecutive calls will generally be similar, and one would expect the best value of the tilde parameters from the previous setting of the hyperparameters as a reasonable starting guess. (If it turns out that this strategy leads to a very bad marginal likelihood value, then the function reverts to starting at zero.)

The Expectation Propagation implementation follows Algorithm 3.5, section 3.6, page 58

The iterations are terminated when the improvement in log marginal likelihood drops below a small tolerance, or a prespecified maximum (10) number of sweeps is reached (causing a warning message to be issued). About five sweeps is often sufficient when starting from zero, less if a reasonable starting point is available.

Alternatively, if we are in the training mode, we proceed to compute the partial derivatives of the log marginal likelihood wrt the hyperparameters, using Algorithm 5.2, section 5.5, page 127

Example of Laplace's Approximation applied to a 2-dimensional classification problem

You can either follow the example below or run the short demo_ep_2d.m script. First we generate a simple artificial classification dataset, by sampling data points from each of two classes from separate Gaussian distributions, as follows:

  n1=80; n2=40;                         % number of data points from each class
  randn('seed',17)

  S1 = eye(2); S2 = [1 0.95; 0.95 1];             % the two covariance matrices
  m1 = [0.75; 0]; m2 = [-0.75; 0];                              % the two means

  x1 = chol(S1)'*randn(2,n1)+repmat(m1,1,n1);          % samples from one class
  x2 = chol(S2)'*randn(2,n2)+repmat(m2,1,n2);              % and from the other

  x = [x1 x2]';                                      % these are the inputs and
  y = [repmat(-1,1,n1) repmat(1,1,n2)]';         % outputs used a training data

Below the samples are show together with the "Bayes Decision Probabilities", obtained from complete knowledge of the data generating process:

Note, that the ideal predictive probabilities depend only on the relative density of the two classes, and not on the absolute density. We would eg expect that the structure in the upper right hand corner of the plot may be very difficult to obtain based on the samples, because the data density is very low. The contour plot is obtained by:

  [t1 t2] = meshgrid(-4:0.1:4,-4:0.1:4);
  t = [t1(:) t2(:)];                                % these are the test inputs

  tt = sum((t-repmat(m1',length(t),1))*inv(S1).*(t-repmat(m1',length(t),1)),2);
  z1 = n1*exp(-tt/2)/sqrt(det(S1));
  tt = sum((t-repmat(m2',length(t),1))*inv(S2).*(t-repmat(m2',length(t),1)),2);
  z2 = n2*exp(-tt/2)/sqrt(det(S2));

  contour(t1,t2,reshape(z2./(z1+z2),size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

Now, we will fit a probabilistic Gaussian process classifier to this data, using an implementation of the Expectation Propagation (EP) algorithm. We must specify a covariance function. First, we will try the squared exponential covariance function covSEiso. We must specify the parameters of the covariance function (hyperparameters). For the isotropic squared exponential covariance function there are two hyperparameters, the lengthscale (kernel width) and the magnitude. We need to specify values for these hyperparameters (see below for how to learn them). Initially, we will simply set the log of these hyperparameters to zero, and see what happens. For the likelihood function, we use the cumulative Gaussian:

  loghyper = [0; 0];
  p2 = binaryEPGP(loghyper, 'covSEiso', x, y, t);
  clf
  contour(t1,t2,reshape(p2,size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

to produce predictive probabilities on the grid of test points:

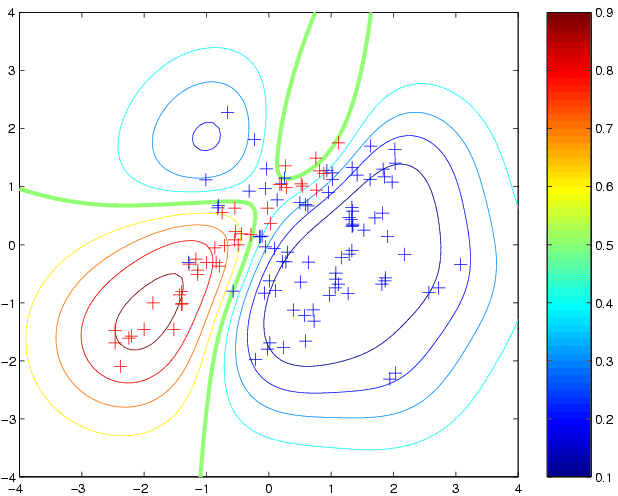
  newloghyper = minimize(loghyper, 'binaryEPGP', -20, 'covSEiso', x, y)
  p3 = binaryEPGP(newloghyper, 'covSEiso', x, y, t);

  clf
  contour(t1,t2,reshape(p3,size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

produces:

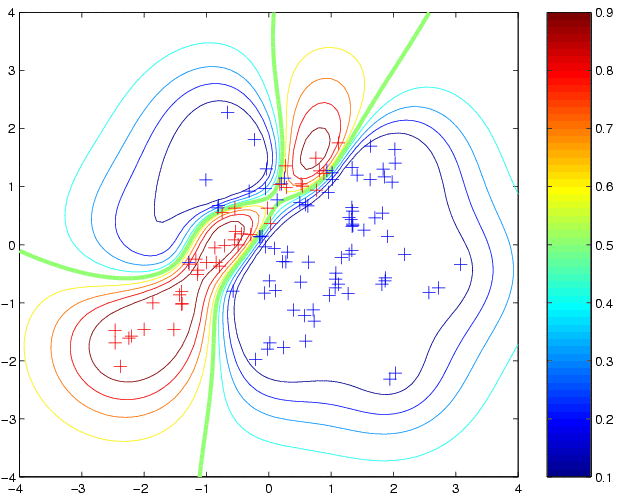
Note, that this plot still shows that the predictive probabilities revert to one half, when we move away from the data (in stark contrast to the "Bayes Decision Probabilities" in this example). This may or may not be seen as an appropriate behaviour, depending on our prior expectations about the data. It is a direct consequence of the behaviour of the squared exponential covariance function. We can instead try a neural network covariance function, which has the ability to saturate at specific latent values, as we move away from zero:

  newloghyper = minimize(loghyper, 'binaryEPGP', -20, 'covNN', x, y);
  p4 = binaryEPGP(newloghyper, 'covNN', x, y, t);
  clf
  contour(t1,t2,reshape(p4,size(t1)),[0.1:0.1:0.9]);
  hold on
  plot(x1(1,:),x1(2,:),'b+')
  plot(x2(1,:),x2(2,:),'r+')

to produce:

which shows extreme probabilities even at the boundaries of the plot.

Example of the Expectation Propagation Algorithm applied to hand-written digit classification

You can either follow the example below or run the short demo_ep_usps.m script. You will need the code form the gpml-matlab.tar.gz archive and additionally the data, see below. Consider compiling the mex files (see README file), although the programs should work even without.

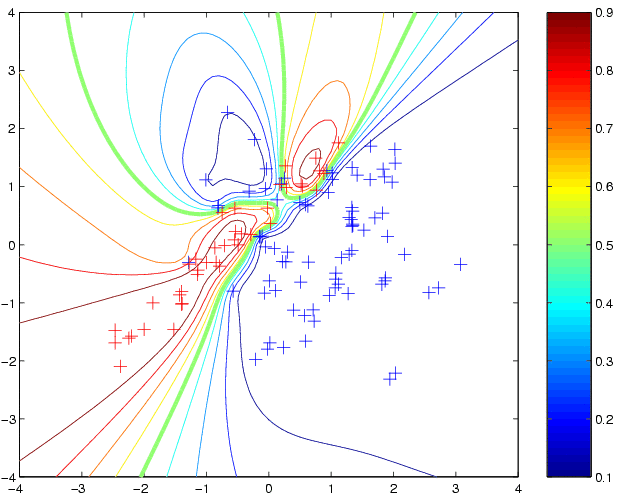
  cd gpml-demo                      % you need to be in the gpml-demo directory
  cd ..; w=pwd; addpath([w,'/gpml']); cd gpml-demo  % add the path for the code
  [x y xx yy] = loadBinaryUSPS(3,5);

Now, let us make predictions using the squared exponential covariance function covSEiso. We must specify the parameters of the covariance function (hyperparameters). For the isotropic squared exponential covariance function there are two hyperparameters, the lengthscale (kernel width) and the magnitude. We need to specify values for these hyperparameters (see below for how to learn them). One strategy, which is perhaps not too unreasonable would be to set the characteristic length-scale to be equal to the average pair-wise distance between points, which for this data is around 22; the signal variance can be set to unity, since this is the range at which the sigmoid non-linearity comes into play. Other strategies for setting initial guesses for the hyperparameters may be reasonable as well. We need to specify the logarithm of the hypers, roughly log(22)=3 and log(1)=0:

  loghyper = [3.0; 0.0];   % set the log hyperparameters
  p = binaryEPGP(loghyper, 'covSEiso', x, y, xx);

which may take a few minutes to compute. We can visualize the predictive probabilities for the test cases using:

  plot(p,'.')
  hold on
  plot([1 length(p)],[0.5 0.5],'r')

to get:

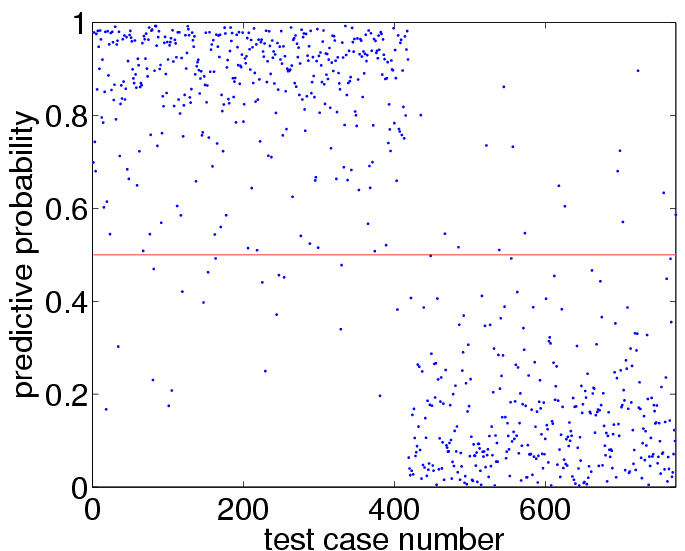
  sum((p>0.5)~=(yy>0))
  mean((yy==1).*log2(p)+(yy==-1).*log2(1-p))+1

which shows test set 35 prediction errors (out of 773 test cases) and an average amount of information of about 0.72 bits, compare to Figure 3.8(b) and 3.8(d) on page 65.

More interestingly, we can also use the program to find the values for the hyperparameters which optimize the marginal likelihood, as follows:

  [loghyper' binaryEPGP(loghyper, 'covSEiso', x, y)]
  [newloghyper logmarglik] = minimize(loghyper, 'binaryEPGP', -20, 'covSEiso', x, y);
  [newloghyper' logmarglik(end)]

where the third argument -20 to the minimize function, tells minimize to evaluate the function at most 20 times (this is adequate when the parameter space is only 2-dimensional. Warning: the optimization above may take about an hour depending on your machine and whether you have compiled the mex files. If you don't want to wait that long, you can train on a subset of the data (but note that the cases are ordered according to class).

Above, we first evaluate the negative log marginal likelihood at our initial guess for loghyper (which is about 222), then minimize the negative log marginal likelihood w.r.t. the hyperparameters, to obtain new values of 2.55 for the log lengthscale and 3.96 for the log magnitude. The negative log marginal likelihood decreases to about 90 at the minimum, see also Figure 3.8(a) page 65. The negative log marginal likelihood decreases to about 90 at the minimum, see also Figure 3.7(a) page 64. The marginal likelihood has thus increased by a factor of exp(222-90) or roughly 2e+57.

Finally, we can make test set predictions with the new hyperparameters:

  pp = binaryEPGP(newloghyper, 'covSEiso', x, y, xx);
  plot(pp,'g.')

to obtain:

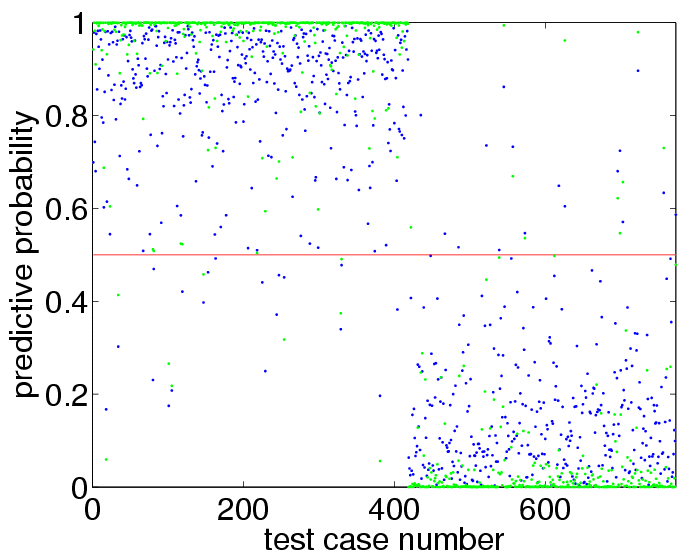
We note that the new predictions (in green) are much more extreme than the old ones (in blue). Evaluating the new test predictions:

  sum((pp>0.5)~=(yy>0))
  mean((yy==1).*log2(pp)+(yy==-1).*log2(1-pp))+1

reveals that there are now 19 test set misclassifications (as opposed to 35) and the information about the test set labels has increased from 0.72 bits to 0.89 bits.

Go back to the web page for Gaussian Processes for Machine Learning.

Last modified: Thu Mar 23 15:23:00 CET 2006