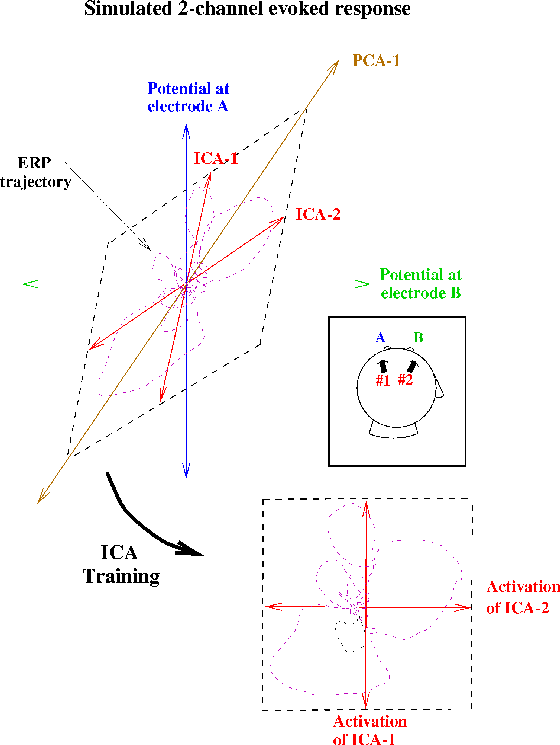
Figure 1b. (Square inset) Schematic illustration of ICA decompositions of a simulated evoked response, recorded at two electrodes (A and B), summing the activity of two temporally independent response sources (#1 and #2) with arbitrary (focal or diffuse) spatial distributions (Upper plot). Scatterplot of potentials recorded at the two electrodes, showing the response as a 2-dimensional trajectory. In this plot, the activity of source #1 alone would lie on the near-vertical axis ICA-1; the activity of source #2 alone would lie on the near-horizontal (but not orthogonal) axis ICA-2. If the time courses of activation of the two brain networks are independent of one another, the summed output of sources #1 and #2 will, over time, fill the dashed parallelogram. The first principal component of the data (PCA-1) indicates the direction of maximum data variance, but no principal component identifies either of the independent components. The ICA algorithm finds the directions of the two axes (ICA-1, ICA-2) by maximizing the entropy of a nonlinear transform of the data following linear transformation to the ICA component axes (Lower plot), i. e., the linear transformation and sigmoidal nonlinearity rotates and spreads apart the data to maximally fill the dashed square.

The Independent Component Analysis algorithm

The ICA algorithm we use {BellSej95, BS95b} (Fig. 1) is based on an `infomax' neural network {Lin92, NP94}. It finds, by stochastic gradient ascent, a matrix, W, which maximizes the entropy {CT91}, H(y), of an ensemble of `sphered' input vectors (xs), linearly transformed and sigmoidally compressed (u=W(xs), y=g(u)). The `unmixing' matrix W performs component separation, while the sigmoidal nonlinearity g() provides necessary higher-order statistical information. Subsequent sphering of the (zero-mean) input data {BS96} ((xs) = Sx, where S = 2^-1/2 speeds convergence. W is then initialized to the identity matrix (I) and iteratively adjusted using small batches of data vectors (normally 10 or more) drawn randomly from (xs) without substitution, according to:

where e is the learning rate (normally less than 0.01) and vector y-hat has elements

The 'WTW' `natural gradient' term in the update equation {CIC94, ACY96} avoids matrix inversions and speeds convergence by normalizing the variance in all directions.

We use the logistic nonlinearity,

which gives a simple update rule,

and biases the algorithm towarding finding sparsely-activated or super-Gaussian independent components with positive kurtosis {Ols96}, consonant with the assumption that ERPs are composed of one or more overlapping series of brief activations within spatially fixed brain networks performing separable stages of stimulus information processing. The algorithm is able to accurately decompose sums of components with skewed distributions even without making use of nonlinearities specifically tailored to them {BellSej95}.

The ICA algorithm is easily implemented and computationally efficient. The present implementation does not require matrix inversions, making it practical for use on data from a hundred or more channels. The number of time points needed for the method may be as few as several times the number of recording channels, which in turn must be at least equal to the number of components to be separated. The rows of the output data matrix, u, are the activation waveforms of the ICA components, while the columns of the inverse matrix,

of the overall transformation, WS, give the projection strengths of the respective components onto the scalp sensors. The data accounted for by the ith component is the outer product,

of the ith component activation with the ith column of the inverse matrix. Scaling information is distributed between the activation waveforms, u(i), and the maps, hence relative component strengths can only be compared via their projections. Note that care must be taken in interpreting decompositions of data sets in which the channel means are far from the baseline means. This ICA algorithm is one of a family of algorithms that exploit independence to perform blind separation {BS95b, CIC94, ACY96, Com94, JH91, KO00, CL00, PP96}.

Application to evoked response decomposition

The ICA algorithm was applied to two 14-channel, 1-sec (312-point) averaged ERPs time locked to detected and undetected targets, respectively, presented in an experiment in which the subject responded by pressing a button each time he heard a weak, slow-onset noise-burst (mean rate, 10/min; duration, 350 ms; rise time, 150 ms; intensity, 6 dB sensation level) embedded in a continuous (62 dB) noise background containing a 39-Hz click train producing a steady-state response (SSR) {GalMak81}. Target noise-bursts were presented in half the intervals between brief non-target tones (50 ms, 72 dB, 568 Hz, stimulus-onset asynchrony 2-4 s). Further details have been reported elsewhere {MI93}.

EEG was collected from thirteen scalp electrodes referred to the right mastoid, and from a bipolar diagonal electrooculographic placement with a sampling rate of 312.5 Hz and an analog pass band of 0.1-100 Hz. During the 28-min session, the subject experienced variably increasing drowsiness while his target detection rate declined from 100% to 40%. After rejecting trials containing electrooculographic (EOG) potentials larger than 70 uV, brain responses to detected and undetected targets were averaged separately, giving two 312-point ERPs.

ICA decomposition was performed simultaneously on all 624 time points of both ERPs using Matlab 4.21 on a Sun HyperSparc 125 MHz processor. The learning batch size was 10. Initial learning rate was 0.006. Learning rate was gradually reduced to 10^-6 during 50 training iterations taking 7 sec of computer time. The input data is available via http with a package of Matlab routines for performing the analysis\ddag.

Results

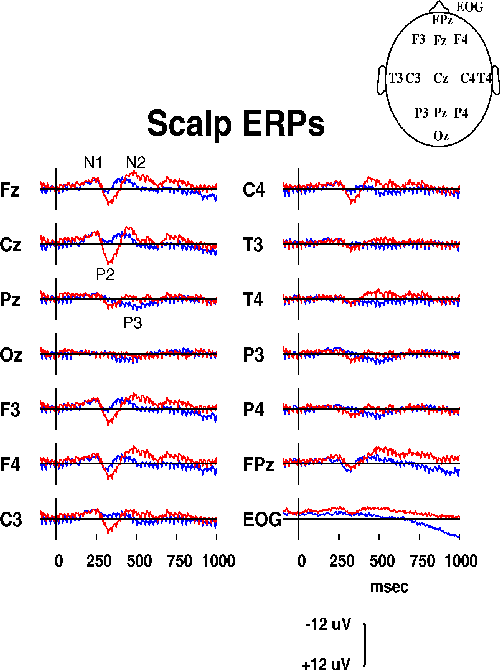
The two responses to detected and undetected targets (Fig. 2a) contained the standard auditory response peaks N1, P2, and N2, although the N1 peak was indistinct, most probably because of the long rise time of the noise-burst stimulus and the variable noise background.

Figure 2a. Responses at 14 scalp channels from one subject in a sustained auditory detection experiment{MI93} to detected (blue traces, N=209) and undetected (red traces, N=81) slow-onset noise-burst targets.

As expected from sleep studies of auditory evoked responses {VS94}, the P2 and N2 peaks were larger and had longer latencies in response to undetected targets. The detected-target response also had a parietal P3 component (quite small in this subject), and both responses contained a robust 39-Hz SSR in all channels. The EOG channel showed some residual ocular activity spreading into frontal sites (see, e.g., Fpz). Absolute correlations between chanels averaged 0.604 (range: 0.001 to 0.987). Differences between the channel and baseline means were small.

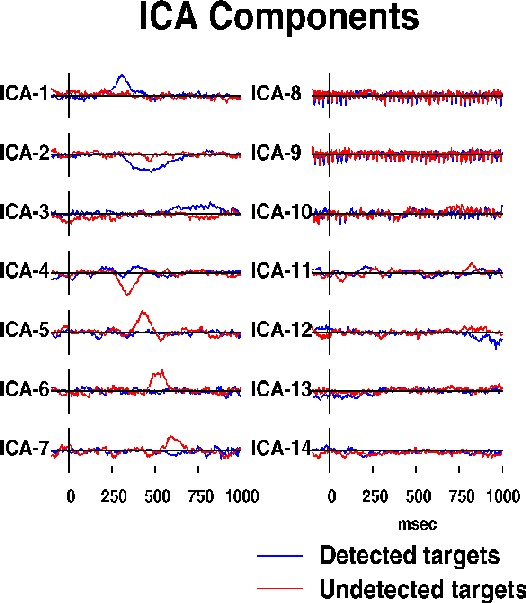
Fig. 2b. Activation wave forms of the resulting 14 ICA components during the detected (blue traces) and undetected (red traces) response epochs. Seven components (ICA-1 to ICA-7) are predominantly activated for 50-300 ms during one or the other response. Three more ICA components (ICA-8 to ICA-10) compose the auditory steady-state response (SSR){GalMak81} to a click train presented throughout the experiment at one-eighth the EEG sampling rate. The remaining four ICA components (ICA-11 to ICA-14) presumably sum activity of multiple weak brain and extra-brain sources.

The ICA algorithm was used to simultaneously decompose the two 1-sec ERPs into 14 ICA components whose activation waveforms are shown in Fig. 2b. Although the algorithm used no temporal sequence information, seven of the ICA components (ICA-1 to ICA-7) were active in a single 50-300 msec interval in one of the response conditions. One of these (ICA-4) was active in both conditions. Three more ICA components (ICA-8 to ICA-10) were predominantly periodic at the 39 Hz SSR driving rate. Absolute residual correlations between activation waveforms of these ten ICA components averaged 0.034, ranging from 0.0001 to 0.143. Projection of these ten components onto the scalp array accounted for 96.8% of total response variance. Four remaining ICA components (ICA-11 to ICA-14), had higher residual correlations (mean 0.093, range 0.009 to 0.207) and more complex scalp maps (not shown) suggesting they accounted for mainly for residual ocular and muscle activity.

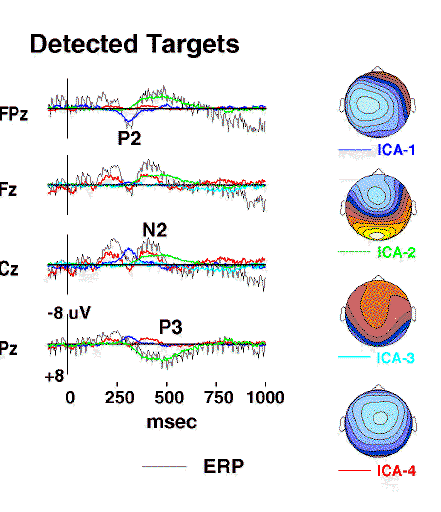
Figure 3a. Projected activity of components ICA-1 to ICA-4 (colored traces) superimposed on the scalp wave forms of the detected-target response (grey traces) together with interpolated topographic maps of the component projections{Perrin89}. Component ICA-2 (green traces) accounts for the central parietal positivity near 450 ms (labeled P3) as well as the concurrent prefrontal positivity at Fpz, whereas the central negativity near 400 msec (labeled N2) includes the activity of component ICA-4 (red traces) which has a different scalp distribution (map scaling +/-6 uV).

Figs. 3a and 3b shows projections of the first seven components to selected scalp electrodes. The detected-target P2 and P3 peaks and the undetected-target P2 were accounted for by single ICA components, while the algorithm decomposed the N2 peak in each response into two or more ICA components. Maps of the individual component scalp projections contained one or two spatial extrema and clearly distinguished components having central, frontal, and periocular foci, even when these appeared to form a single broad peak in the response waveforms at some sites (e.g. ICA5 to ICA-7). Component ICA-2 accounted for both the detected-target P3 waveform at site Pz and the parallel late negativity at site Fpz. A component with similar time course and topography was found for other subjects in the experiment (Fig. 3d). Component ICA-4 accounted for much of the P2 and early-N2 complex in the detected-target response, but only the central-P2 peak in the undetected-target response.

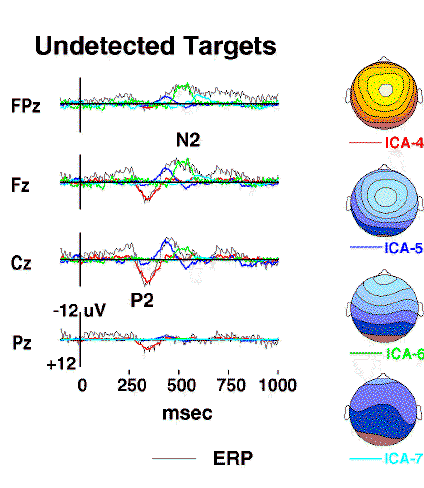
Figure 3b. Projected scalp activity of components ICA-4 to ICA-7 (colored traces) superimposed on the scalp wave forms of the undetected-target response (grey traces). The positive central peak near 300 ms (labeled P2) is accounted for by a single component ICA-4 (red traces), whereas the succeeding frontal negativity (labeled N2) is decomposed by the algorithm into three other components (ICA-5 to ICA-7) having central, frontal, and periocular topographies, respectively (map scaling +/-12 uV).

Fig. 3c shows averaged single-cycle SSRs computed by averaging all SSR cycles in the detected-target ERP and in the scalp projections of the 3 periodic ICA components. SSR waveforms for all 14 channels are superimposed. Above each of the three ICA SSR components is the map associated with each component. The map of the largest component (ICA-8) strongly resembled the topography of the whole SSR at its amplitude peak (not shown). Components ICA-9 and ICA-10 accounted for differences in SSR topography at other time points.

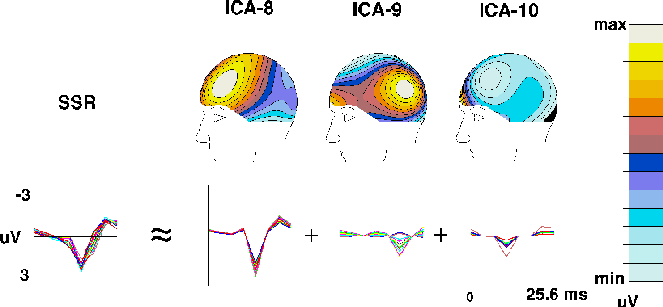
Figure 3c. The ICA algorithm decomposes the 39-Hz auditory SSR in the detected-target response into three components (ICA-8 to ICA-10) derived from the detected-target ERP (Fig. 2a) by averaging 39 successive 25.6-ms (8-point) ERP time segments. The leftmost traces show the whole SSR at all 14 channels, the right traces the projected time wave forms and scalp projections (scaled individually) of the three ICA components. Component ICA-8 has a bilateral frontal scalp distribution as expected{Pantev93}, while component ICA-9 has a bilateral parietal scalp distribution and component ICA-10 projects mainly to EOG and prefrontal channels.

Stability of the decomposition

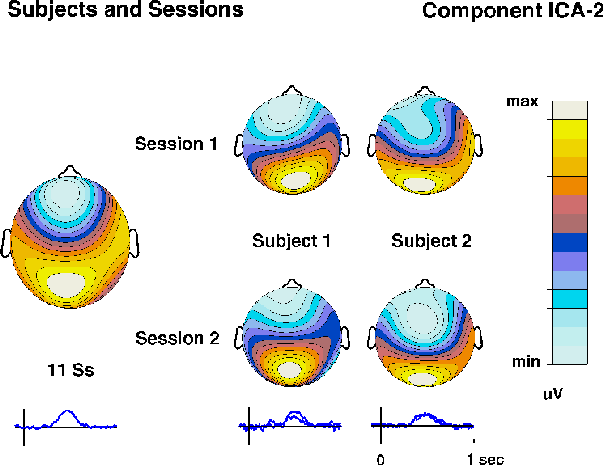
Fig. 3d. Time courses and topographies of corresponding ICA-2 components obtained in separate decompositions of detected-target responses in two separate sessions from two subjects (right columns) and from the grand-mean detected-target response for 11 subjects (left column). Note the nearly identical time courses (right traces) and scalp maps.

The activation waveforms and scalp maps of the ICA components with largest projected activities were relatively robust to changes in initial weights, the number of training conditions, and even the number and placement of electrodes. For example, decomposing the data in Fig. 2a using arbitrary subsets of 11 of the 14 channels gave components whose activations and scalp projections correlated 0.9 or above with ICA components 1, 4, 5, 6, 8, and 9 of Fig. 2b.

ICA decompositions of electric and magnetic evoked responses to a variety of stimuli from several experiments (unpublished) proved similar in character and stability. The algorithm is particularly effective at detecting common response topography in multiple response conditions, and quantifying differences between conditions in activation strength of multiple components.

Relation to traditional peak analysis

ERP components usually are identified with individual event-related response peaks (e.g. N1, P2, N2, etc.) which were first supposed to represent the activities of brain areas involved in discrete stages of information processing. However even the peaks of a response waveform may sum the spatially and temporally overlapping activities from two or more brain areas with different time courses of activation {NaatPict87}. When this happens, the scalp topography of the response appears to move continuously even when the brain locations of the active generators are fixed, producing different peak latencies at each scalp site. This is incompatible with the assumption that each peak represents a single response component arising in a fixed brain area. ICA accounts for channels differences in ERP peak latencies by decomposing the activity under each peak into two or more ICA components, each having a spatially fixed scalp topography.

Relation to Principal Component Analysis

Another linear transformation method previously proposed for ERP decomposition {ChapMcC95}, Principal component analysis (PCA), finds orthogonal directions of greatest variance in the data, whereas ICA finds nearly temporally-independent (not just uncorrelated) components whose maps may be non-orthogonal (Fig. 1b). Principal components of data generated by temporally sparse and independent, but spatially non-orthogonal sources will be linear combinations of activity in all the sources, whereas ICA components of the data will individually identify the larger sources. The proposed Varimax extension of the PCA method rotates the PCA vectors to maximize the variance of their activation waveforms {ChapMcC95}. However, the relevance of this criterion to ERP genesis is unclear. Applying PCA to the ERP data in Fig. 2a, either alone or followed by Varimax rotation, produced components active throughout both responses (unpublished) with minimal correspondence to the ICA components. When evoked brain activity arises through temporally distinct or partially overlapping activations of independently-active neural populations, then ICA appears to be a more appropriate method for separating their contributions to scalp data.

Discussion

The exploratory use of ICA decomposition for ERP analysis is based on three assumptions: (1) that summation at scalp electrodes of potentials arising in different brain areas is linear; (2) that ERPs are largely the sum of relatively-brief activations in a restricted set of spatially-stable brain areas, networks, or neural populations; (3) that the time-courses of activation are largely temporally-independent. The first two assumptions appear reasonable. The third assumption limits the decomposition to temporally independent components.

To explore the strengths and limitations of the method, we ran a number of numerical simulations in which 600-point signals recorded from the cortex of a patient during preparation for operation for epilepsy were projected to simulated scalp electrodes through a three-shell spherical model {Tech-2, Tech-1}. We used electrocorticographic data in these simulations as a plausible best approximation to the temporal dynamics of the unknown ERP brain generators. Results confirmed that the ICA algorithm could accurately identify the activation waveforms and scalp topographies of relatively large and more temporally-independent simulated sources, even in the presence of a large number of small and temporally independent simulated sources.

However, given simulated ERP activity arising from separate brain generators whose time courses of activation were made substantially correlated, the algorithm parsed the resulting continuously-varying scalp responses into distributed activity within overlapping subsets of the simulated sources {Tech-2}. Similarly, SSR components ICA-8 and ICA-9 (Fig. 3c) collected synchronous bilateral SSR activity instead of splitting it into components with left- and right-sided topographies, and the neural populations generating the activities accounted for by two spatially overlapping components, for example ICA-4 and ICA-5 (Fig. 3b), might not be disjoint since their scalp distributions are so similar. More generally, given data summing components (however defined) that are not temporally independent, spatially fixed, or sparsely activated, or whose number is not the same as the number of data channels, the algorithm will not reproduce the original component distribution, and other linear blind separation algorithms may produce somewhat different results.

Note that for data sets in which the channel means differ significantly from the baseline means, removing the channel mean offsets prior to analysis introduces into the decomposition an implicit DC component without physiological significance. Methods for dealing with such data sets will be presented elsewhere.

The range of ERP components that can be separated by the algorithm is illustrated by the single broad component (ICA-2), accounting for the posterior P3 response to detected targets as well as the accompanying anterior negativity (Fig. 3a), and the three near-periodic ICA components (ICA8, ICA-9, ICA-10) that together accounted for 95.3% of the total SSR (Fig. 3c). This ICA decomposition of the auditory SSR into three spatially-fixed components contrasted sharply with a previously proposed interpretation that spatial SSR instability reflects a moving crest of activity sweeping through cortex every 25 msec {LR93}. By itself, however, ICA cannot be used to decide between these or other source models {Pantev93, ION91}.

Conclusions

ICA decomposition opens a new and potentially useful window into complex event-related brain data that can complement other analysis techniques. Further research will be required to fully assess the value and limitations of temporal independence as a segregation criterion. Blind separation by ICA decomposition appears promising for multidimensional measurement of the effects of experimental variables on electric and magnetic evoked-response components representing rapid and discrete stages of brain information processing, particularly when these overlap in scalp distribution. The method may be especially effective for comparing the activations of brain response components that are differentially activated in several related stimulus and cognitive task conditions. Although it may be difficult to locate ICA components within the brain on the basis of their time courses and scalp projections, ICA decomposition might nonetheless prove useful for preprocessing data prior to applying source localization algorithms. ICA decomposition may be useful as well for observing event-related changes in the spatial structure of correlated ongoing EEG activity in multiple brain areas {Bullock95, Gevins, Lehmann, Rappels, Venky96}. The method should be equally applicable to magnetoencephalographic (MEG) data, and can be generalized to track changes in the spatial structure of EEG or MEG activity in different brain states {MB96}.

References

Aine, C. J., A conceptual overview and critique of functional neuroimaging techniques in humans: I. MRI/FMRI and PET. Crit. Rev. Neurobiol. 9, 229-309 (1995).

Snyder, A. Z., Abdullaev, Y. G., Posner, M. I. & Raichle, M. E., Scalp electrical potentials reflect regional cerebral blood flow responses during processing of written words. Proc. Natl. Acad. Sci. USA 92, 1689-1693 (1995).

Makeig, S. & Inlow, M., Lapses in alertness: Coherence of fluctuations in performance and EEG spectrum. Electroencephalogr. clin. Neurophysiol. 86, 23-35 (1993)

Naatanen, R. & Picton, T., The N1 wave of the human electric and magnetic response to sound: a review and an analysis of the component structure. Psychophysiology 24, 375-425 (1987).

Nunez, P.L., Electric Fields of the Brain. New York: Oxford (1981).

Scherg, M. & Von Cramon, D., Evoked dipole source potentials of the human auditory cortex. Electroencephalogr. Clin. Neurophysiol. 65, 344-601 (1986).

Dale, A.M. & Sereno, M.I., Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction - a linear approach. J. Cogn. Neurosci. 5, 162-176 (1993).

Chapman, R.M. & McCrary, J.W., EP component identification and measurement by principal components analysis. Brain Lang. 27, 288-301 (1995).

Bell, A.J. & Sejnowski, T.J., An information-maximization approach to blind separation and blind deconvolution, Neural Computation 7, 1129-1159 (1995).

Makeig, S., Bell, A.J., Jung, T-P. & Sejnowski T.J., Independent component analysis of electroencephalographic data. Advances in Neural Information Processing Systems 8, 145-151, MIT Press (1996).

Linsker, R., Local synaptic learning rules suffice to maximise mutual information in a linear network. Neural Computation 4, 691-702 (1992).

Nadal, J-P. & Parga, N., Non-linear neurons in the low noise limit: a factorial code maximises information transfer. Network 5, 565-581 (1994).

Cover, T.M. & Thomas, J.A., Elements of Information Theory John Wiley (1991).

Bell, A.J. & Sejnowski, T.J., Learning the higher-order structure of a natural sound, Network: Computation in Neural Systems 7, 2 (1996).

Cichocki A., Unbehauen R., & Rummert E., Robust learning algorithm for blind separation of signals, Electronics Letters 30, 1386-1387 (1994).

Amari S., Cichocki, A. & Yang, H.H., A new learning algorithm for blind signal separation. In: Advances in Neural Information Processing Systems 8, MIT Press (1996).

Galambos, R., Makeig, S. & Talmachoff P., A 40 Hz auditory potential recorded from the human scalp, Proc. Natl. Acad. Sci. USA 78, 2643-2647 (1981).

Makeig, S., Jung, T-P., Ghahremani, D. & Sejnowski, T.J., Independent Component Analysis of Simulated ERP Data. Tech. Rep. INC-9606, Institute for Neural Computation, San Diego, CA. (1996).

Ghahremani, D., Makeig, S., Jung, T-P., Bell, A.J. & Sejnowski, T.J., Independent Component Analysis of Simulated EEG Using a Three-Shell Spherical Head Model. Tech. Rep. INC-9601, Institute for Neural Computation, San Diego, CA. (1996).

Bullock, T. H., McClune, M. S., Achimowicz, J. Z., Iragui-Madoz, V. J., Duckrow, R. B. & Spencer, S. S., Temporal fluctuations in coherence of brain waves. Proc. Natl. Acad. Sci. USA 92, 11568-11572 (1995).

Gevins, A., High resolution evoked potentials of cognition. Brain Topography 8, 189-199 (1996).

Wackermann, J,, Lehmann, D., Michel, C. M., & Strik, W. K., Adaptive segmentation of spontaneous EEG map series into spatially defined microstates. Int. J. Psychophysiol. 14, 269-83 (1993).

Rappelsberger, P., Pfurtscheller, G., & Filz, O., Calculation of event-related coherence--a new method to study short-lasting coupling between brain areas. Brain Topography 7, 121-127 (1994).

Bell, A.J. & Sejnowski, T.J., Fast blind separation based on information theory. Proc. Intern. Symp. on Nonlinear Theory and Applications, Las Vegas (1995).

Comon, P., Independent component analysis, a new concept? Signal Processing 36, 287-314 (1994).

Jutten, C. & Herault, J., Blind separation of sources, part I: an adaptive algorithm based on neuromimetic architecture. Signal Processing 24, 1-10 (1991).

Karhumen, J., Oja, E., Wang, L., Vigario, R. & Joutsenalo, J., A class of neural networks for independent component analysis, IEEE Trans. Neural Networks (to appear).

Cardoso, J-F. & Laheld, B., Equivalent adaptive source separation, IEEE Trans. Signal Proc. (to appear).

Perrin, F., Pernier, J., Bertrand, O., & Echallier, J.F., Spherical splines for scalp potential and current density mapping. Electroencephalogr. Clin. Neurophysiol. 72, 184-187 (1989).

Pantev, C., Elbert, T., Makeig, S., Hampson, S., Eulitz, C. & Hoke, M., Relationship of transient and steady-state auditory evoked fields. Electroencephalogr. clin. Neurophysiol. 88, 389-396 (1993).

Venkatesh, N. Murthy & Fetz, E., Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys J. Neurophysiol. 76, 3968-3982 (1996).

Olshausen, B. C.B.C.L. Paper 138, Dept. of Brain and Cognitive Sciences, MIT (1996).

Llinas, R, & Ribary, U., Coherent 40-Hz oscillation characterizes dream state in humans. Proc. Nat. Acad. Sci. USA 90:2078-81 (1993).

Hillyard, S. A. & Munte, T. F., Selective attention to color and location: an analysis with event-related brain potentials. Percept. Psychophys., 36, 185-98 (1984).

Van Sweden, B., Van Dijk, J. G. & Caekebeke, J. F., Auditory information processing in sleep: late cortical potentials in an oddball paradigm. Neuropsychobiology, 29:152-6 (1994).

Pearlmutter, B. A. & Parra, L. C., A context-sensitive generalization of ICA. International Conference on Neural Information Processing, Hong Kong (1996).

Ribary, U., Ioannides, A. A., Singh, K. D., Hasson, R., Bolton, J. P., Lado, F., Mogilner, A. & Llinas R. Magnetic field tomography of coherent thalamocortical 40-Hz oscillations in humans. Proc. Nat. Acad. Sci. USA 88:11037-11041 (1991).

Acknowledgments

This report was supported in part by grants to S.M., T-P.J. and T.J.S. from the Office of Naval Research, and to T.J.S. from the Howard Hughes Medical Institute. The authors acknowledge F.S. Elliott and M. Inlow for help in collecting and processing the data, A. Dale for supplying the head model, and M. McKeown, S. Hillyard, L. Anllo-Vento, and J. Hansen for discussions and assistance with graphics.