Blind Separation of Auditory Event-related Brain
Responses into Independent Components
Scott Makeig(1,3), Tzyy-Ping Jung(2),Responses into Independent Components
Anthony J. Bell(2), Dara Ghahremani(2),
Terrence J. Sejnowski(2,4)
View this paper here in .html (with large figures)
or else
View/Download PDF (.pdf, 3.2Mb)
-
Matlab toolbox for Independent Component Analysis (ICA)
of EEG/MEG data
-
Online Tutorial on the Matlab toolbox
-
Tony Bell's math background papers,
kernal code, alternative ICA approaches -
Publications on ICA applied to EEG and fMRI data
-
Data set from this paper
Sums of slightly different numbers of trials.
(in .txt.tar.gz format, 48K)
formerly
(2)Howard Hughes Medical Institute
(3)Department of Neurosciences
(4)Department of Biology
(1)Naval Health Research Center
San Diego, CA
currently
Computational Neurobiology Laboratory
10010 N. Torrey Pines Rd.
The Salk Institute
La Jolla CA 92037
and
Institute for Neural Computation
University of California San Diego
Computational Neurobiology Laboratory
The Salk Institute, P. O. Box 85800
San Diego, CA ~92186-5800
School of Medicine
University of California San Diego
La Jolla, CA 92093
University of California San Diego
La Jolla, CA 92093
Abstract
Averaged event-related potential (ERP) data recorded from the human scalp reveals electroencephalographic (EEG) activity that is reliably time-locked and phase-locked to experimental events. We report here the application of a method based on information theory that decomposes one or more ERPs recorded at multiple scalp sensors into a sum of components with fixed scalp distributions and sparsely-activated, maximally independent time courses. Independent Component Analysis (ICA) decomposes ERP data into a number of components equal to the number of sensors. The derived components have distinct but not necessarily orthogonal scalp projections. Unlike dipole-fitting methods, the algorithm does not model the locations of their generators in the head. Unlike methods that remove second-order correlations, such as principal component analysis (PCA), ICA also minimizes higher-order dependencies. Applied to detected- and undetected-target ERPs from an auditory vigilance experiment {MI93}, the algorithm derived ten components that decomposed each of the major response peaks into one or more ICA components with relatively simple scalp distributions. Three of these components were active only when the subject detected the targets, three other components only when the target went undetected, and one in both cases. Three additional components accounted for the steady-state brain response to a 39-Hz background click train. Major features of the decomposition proved robust across sessions and changes in sensor number and placement. This new method of ERP analysis can be used to compare responses from multiple stimuli, task conditions, and subject states.
Introduction
Although the locations of the brain areas generating ERPs cannot be uniquely determined by scalp recordings from any number of channels {Nun81}, several methods have been proposed for decomposing evoked responses into activations of distinct neural sources. Most of these also attempt to locate the active areas, either by assuming that they have a known or simple spatial configuration {Scherg}, or that generators are restricted to a small subset of possible locations and orientations {DaleSer93}. Other methods based on rotations of principal components use optimization criteria not directly related to brain anatomy and physiology. These methods may assume that each response component has the same time course of activation in every experimental condition {ChapMcC95}. All these methods use second-order spatiotemporal correlations to perform the decomposition.
Here we report a novel statistical method for decomposing one or more event-related brain responses into a sum of components with spatially fixed scalp distributions and maximally independent (though possibly overlapping) time courses. Independence requires the absence of higher-order as well as second-order correlations between the time courses. Independence, therefore, is a stronger condition than decorrelation and, in particular, is not satisfied by decomposition into principal components by PCA.
Although the neural mechanisms that generate ERPs are not known, the assumptions underlying the application of the ICA algorithm {BellSej95} to ERP data are generally compatible with a widely assumed model. Anatomical and physiological studies have shown that sensory perception and processing occurs in multiple cortical areas, as revealed in many current brain imaging studies {Snyder95}. Averaged ERPs evoked by sensory stimuli and recorded from the scalp are thought to be generated in conjunction with synchronous activity in radially-oriented pyramidal cells in the activated areas. Since volume conduction through the cerebrospinal fluid, skull and scalp is thought to be linear, sensory ERPs are assumed to sum brief and relatively spatially stable potentials associated with synchronous activation of neuropil in each stimulated area.
Activity in neuronal fibers connecting cortical areas does not produce macroscopic fields visible from the scalp. Thus the activity underlying sensory evoked responses has a saltatory character; individual features of sensory ERPs index discrete stages within one or more parallel streams of sensory processing, each stage involving potentials generated in one or more cortical areas. However, the scalp distributions of these generators may overlap in time and space, causing the ERP topography to shift continuously and making decomposition into spatially-fixed activations difficult. For example, if two fixed, dipole-like sources in anterior and posterior cortex were to have spatially overlapping activations with a small delay between them, the scalp potentials they generate would have the appearance of a wave sweeping from front to back on the scalp.
When subjects process sensory signals for their meaning or task relevance, later features appear in the ERP whose spatial scalp patterns are often inconsistent with an origin in sensory cortex. These are believed to index the later cognitive processing of relevant stimulus attributes or information within frontal, inferior, or possibly widespread cortical areas, after this information is first extracted in early sensory areas. A subject's pre-existing level of arousal and attention to the stimuli can also affect the strength of early evoked response components {HM84}.
ICA yields data decompositions consistent with the standard view of ERP genesis outlined above since the spatially-stable and sparsely-active components sum to the observed multichannel responses. ICA determines what spatially fixed and temporally independent component activations compose an observed time-varying response, without attempting to directly specify where in the brain these activations arise. Each ICA component is specified by a fixed linear spatial filter that determines a time course of activation during each response condition, plus a fixed pattern of strengths at each of the scalp electrodes. Data from N electrodes can be reconstructed as the sum of the N independent components.
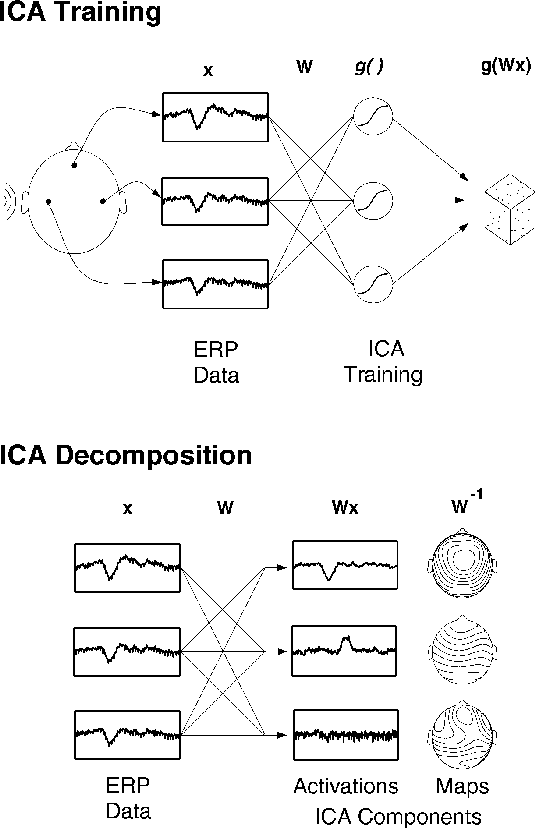
Figure 1a.
Schematic overview of Independent Component Analysis (ICA)
of electroencephalographic (EEG) data.
(Upper panel)
Averaged (or single) EEG epochs, x, recorded from multiple scalp sites
are used to train an `unmixing' weight matrix, W,
so as to maximize the entropy of the
nonlinearly transformed output, g(Wx).
(Lower panel)
After training, rows of the trained weight matrix, W,
are linear spatial filters decomposing the input data into
the independent activities of the ICA components.
Rows of the product of W and the input data, x,
are the activation waveforms of the ICA components,
while columns of the inverse weight matrix, W^{-1},
map their projections onto the sensor array.
Previously, we showed that the ICA algorithm can be used to separate
neural activity from recording and muscle artifacts in spontaneous
EEG data and reported its use for tracking
changes in alertness {MB96}. Here, we use a computationally more
efficient version of the algorithm to decompose relatively brief
evoked brain responses into temporally independent components.
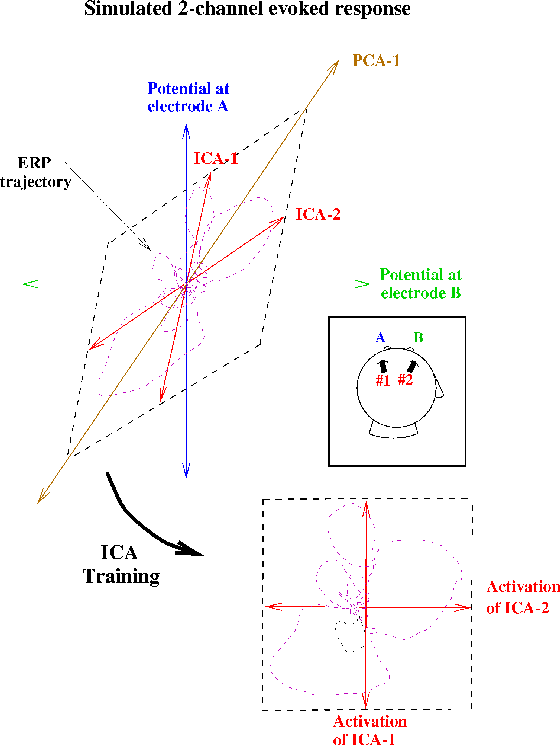
Figure 1b.
(Square inset)
Schematic illustration of ICA decompositions
of a simulated evoked response, recorded at two electrodes (A and B),
summing the activity of two temporally independent response sources
(#1 and #2) with arbitrary (focal or diffuse) spatial distributions
(Upper plot).
Scatterplot of potentials recorded at the two electrodes,
showing the response as a 2-dimensional trajectory.
In this plot, the activity of source #1 alone would lie on the
near-vertical axis ICA-1; the activity of source #2 alone
would lie on the near-horizontal (but not orthogonal) axis ICA-2.
If the time courses of activation of the two brain networks
are independent of one another, the summed output of
sources #1 and #2 will, over time, fill the dashed parallelogram.
The first principal component of the data (PCA-1)
indicates the direction of maximum data variance,
but no principal component identifies
either of the independent components.
The ICA algorithm finds the directions of the two axes
(ICA-1, ICA-2) by maximizing the entropy
of a nonlinear transform of the data
following linear transformation to the ICA component axes
(Lower plot),
i. e., the linear transformation and sigmoidal nonlinearity
rotates and spreads apart the data to maximally fill
the dashed square.
The Independent Component Analysis algorithm
The ICA algorithm we use {BellSej95, BS95b} (Fig. 1) is based on an
`infomax' neural network {Lin92, NP94}. It finds, by stochastic
gradient ascent, a matrix, W, which maximizes the entropy {CT91}, H(y),
of an ensemble of `sphered' input vectors
(xs), linearly transformed and sigmoidally compressed
(u=W(xs), y=g(u)). The `unmixing' matrix W performs
component separation, while the sigmoidal nonlinearity g() provides
necessary higher-order statistical information.
Subsequent sphering of the (zero-mean) input data {BS96} ((xs) = Sx,
where S = 2
where e is the learning rate (normally less than 0.01)
and vector y-hat has elements
The 'WTW' `natural gradient' term in the update
equation {CIC94, ACY96} avoids matrix inversions and speeds
convergence by normalizing the variance in all directions.
We use the logistic nonlinearity,
which gives a simple update rule,
and biases the
algorithm towarding finding sparsely-activated or super-Gaussian
independent components with positive kurtosis {Ols96},
consonant with the assumption that ERPs are composed of one or more
overlapping series of brief activations within spatially fixed brain
networks performing separable stages of stimulus information processing.
The algorithm is able to accurately decompose sums of components with
skewed distributions even without making use of nonlinearities specifically
tailored to them {BellSej95}.
The ICA algorithm is easily implemented and computationally efficient.
The present implementation does not require matrix inversions,
making it practical for use on data from a hundred or more channels.
The number of time points needed for the
method may be as few as several times the number of recording channels,
which in turn must be at least equal to the number of components to be
separated. The rows of the output data matrix, u, are the
activation waveforms of the ICA components, while the columns of the
inverse matrix,
of the overall transformation, WS,
give the projection strengths of the
respective components onto the scalp sensors. The data accounted for by
the ith component is the outer product,
of the ith component activation with the ith column of the
inverse matrix. Scaling information is distributed between the
activation waveforms, u(i), and the maps,
hence relative component strengths
can only be compared via their projections.
Note that care must be taken in interpreting decompositions
of data sets in which the channel means are far from the baseline means.
This ICA algorithm is one
of a family of algorithms that exploit independence to perform blind
separation {BS95b, CIC94, ACY96, Com94, JH91, KO00, CL00, PP96}.
The ICA algorithm was applied to two 14-channel, 1-sec (312-point)
averaged ERPs time locked to detected and undetected targets,
respectively, presented in an experiment in which the
subject responded by pressing a button each time he heard a weak,
slow-onset noise-burst (mean rate, 10/min; duration, 350 ms; rise time,
150 ms; intensity, 6 dB sensation level) embedded in a continuous (62
dB) noise background containing a 39-Hz click train producing a
steady-state response (SSR) {GalMak81}. Target noise-bursts were
presented in half the intervals between brief non-target tones (50 ms,
72 dB, 568 Hz, stimulus-onset asynchrony 2-4 s). Further details have
been reported elsewhere {MI93}.
EEG was collected
from thirteen scalp electrodes referred to the right mastoid, and from a
bipolar diagonal electrooculographic placement with a sampling rate
of 312.5 Hz and an analog pass band of 0.1-100 Hz.
During the 28-min session, the subject experienced variably increasing
drowsiness while his target detection rate declined from 100% to 40%.
After rejecting trials containing electrooculographic (EOG) potentials
larger than 70 uV, brain responses to detected and undetected targets
were averaged separately, giving two 312-point ERPs.
ICA decomposition was performed simultaneously on all 624 time points of both ERPs
using Matlab 4.21 on a Sun HyperSparc 125 MHz processor.
The learning batch size was 10. Initial learning rate was 0.006.
Learning rate was gradually reduced to 10^-6 during 50 training
iterations taking 7 sec of computer time.
The input data is available via http with a package
of Matlab routines for performing the analysis\ddag.
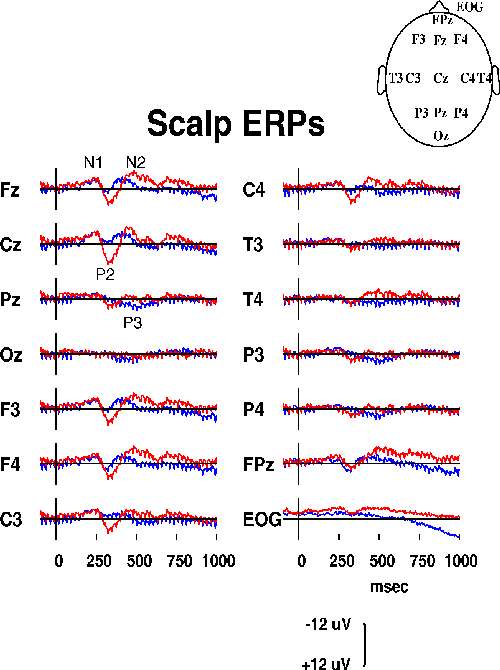
The two responses to detected and undetected targets (Fig. 2a)
contained the standard auditory response peaks N1, P2, and N2,
although the N1 peak was indistinct, most probably
because of the long rise time of the noise-burst stimulus and the
variable noise background.
Figure 2a.
Responses at 14 scalp channels from one subject
in a sustained auditory detection experiment{MI93}
to detected (blue traces, N=209) and undetected
(red traces, N=81) slow-onset noise-burst targets.
As expected from sleep studies of auditory evoked
responses {VS94}, the P2 and N2 peaks were larger and had
longer latencies in response to undetected targets. The detected-target
response also had a parietal P3 component (quite small in this
subject), and both responses contained a robust 39-Hz SSR in all
channels. The EOG channel showed some residual ocular activity
spreading into frontal sites (see, e.g., Fpz). Absolute correlations
between chanels averaged 0.604 (range: 0.001 to 0.987).
Differences between the channel and baseline means were small.
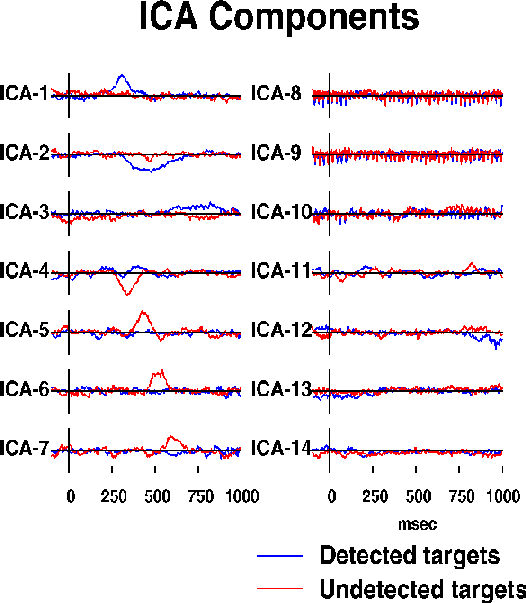
Fig. 2b.
Activation wave forms of the resulting 14 ICA components during
the detected (blue traces) and undetected (red traces) response epochs.
Seven components (ICA-1 to ICA-7) are predominantly activated for 50-300 ms
during one or the other response.
Three more ICA components (ICA-8 to ICA-10) compose
the auditory steady-state response (SSR){GalMak81} to a click train
presented throughout the experiment at one-eighth the EEG sampling rate.
The remaining four ICA components (ICA-11 to ICA-14)
presumably sum activity of multiple weak
brain and extra-brain sources.
The ICA algorithm was used to simultaneously decompose the two 1-sec ERPs
into 14 ICA components whose activation waveforms are shown in Fig. 2b.
Although the algorithm used no temporal sequence information,
seven of the ICA components (ICA-1 to ICA-7) were active in a single
50-300 msec interval in one of the response conditions. One of these
(ICA-4) was active in both conditions. Three more ICA components
(ICA-8 to ICA-10) were predominantly periodic at the 39 Hz SSR driving rate.
Absolute residual correlations between activation waveforms of these ten
ICA components averaged 0.034, ranging from 0.0001 to 0.143.
Projection of these ten components onto the scalp array accounted for
96.8% of total response variance.
Four remaining ICA components (ICA-11 to ICA-14), had higher residual
correlations (mean 0.093, range 0.009 to 0.207) and more complex scalp maps
(not shown) suggesting they accounted for mainly for residual ocular
and muscle activity.
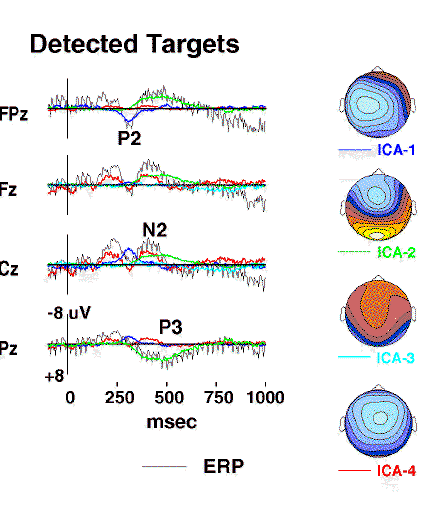
Figure 3a.
Projected activity of components ICA-1 to ICA-4
(colored traces)
superimposed on the scalp wave forms of the detected-target response
(grey traces)
together with interpolated topographic maps
of the component projections{Perrin89}.
Component ICA-2
(green traces)
accounts for the central parietal positivity near 450 ms
(labeled P3)
as well as the concurrent prefrontal positivity at Fpz,
whereas the central negativity near 400 msec
(labeled N2)
includes the activity of component ICA-4
(red traces)
which has a different scalp distribution
(map scaling +/-6 uV).
Figs. 3a and 3b shows projections of the first seven components
to selected scalp electrodes. The detected-target P2 and P3 peaks
and the undetected-target P2 were accounted for by single ICA components,
while the algorithm decomposed the N2 peak in each response into
two or more ICA components.
Maps of the individual component scalp projections contained one or two
spatial extrema and clearly distinguished components
having central, frontal, and periocular foci, even when these
appeared to form a single broad peak in the response waveforms at some sites
(e.g. ICA5 to ICA-7). Component ICA-2 accounted for both the detected-target
P3 waveform at site Pz and the parallel late negativity at site Fpz.
A component with similar time course and topography was found for other
subjects in the experiment (Fig. 3d).
Component ICA-4 accounted for much of the P2 and early-N2 complex
in the detected-target response, but only the central-P2 peak in the
undetected-target response.
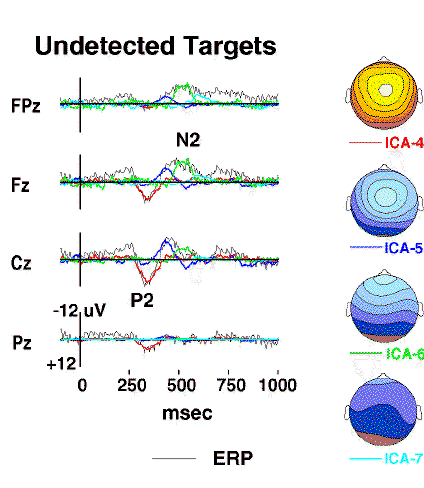
Figure 3b.
Projected scalp activity of components ICA-4 to ICA-7
(colored traces)
superimposed on the scalp wave forms of the undetected-target response
(grey traces).
The positive central peak near 300 ms
(labeled P2)
is accounted for by a single component ICA-4
(red traces),
whereas the succeeding frontal negativity
(labeled N2)
is decomposed by the algorithm into three other components (ICA-5 to ICA-7)
having central, frontal, and periocular topographies, respectively
(map scaling +/-12 uV).
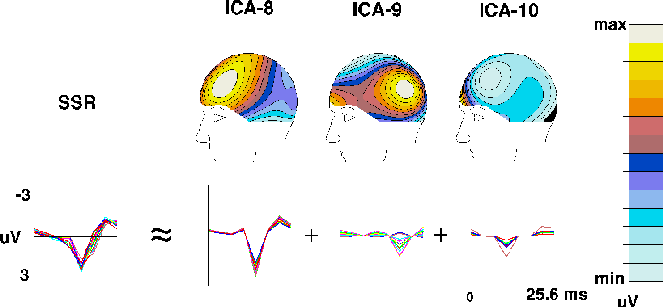
Fig. 3c shows averaged single-cycle SSRs computed by
averaging all SSR cycles in the detected-target ERP and in the scalp
projections of the 3 periodic ICA components. SSR waveforms for all 14
channels are superimposed. Above each of the three ICA SSR components is
the map associated with each component. The map of the largest component
(ICA-8) strongly resembled the topography of the whole SSR at its amplitude
peak (not shown). Components ICA-9 and ICA-10 accounted for differences
in SSR topography at other time points.
Figure 3c.
The ICA algorithm decomposes the 39-Hz auditory SSR
in the detected-target response into three components (ICA-8 to ICA-10)
derived from the detected-target ERP
(Fig. 2a)
by averaging 39 successive 25.6-ms (8-point) ERP time segments.
The leftmost traces show the whole SSR at all 14 channels,
the right traces the projected time wave forms and scalp projections
(scaled individually)
of the three ICA components.
Component ICA-8 has a bilateral frontal scalp distribution
as expected{Pantev93}, while component ICA-9 has
a bilateral parietal scalp distribution
and component ICA-10 projects mainly to EOG and prefrontal channels.
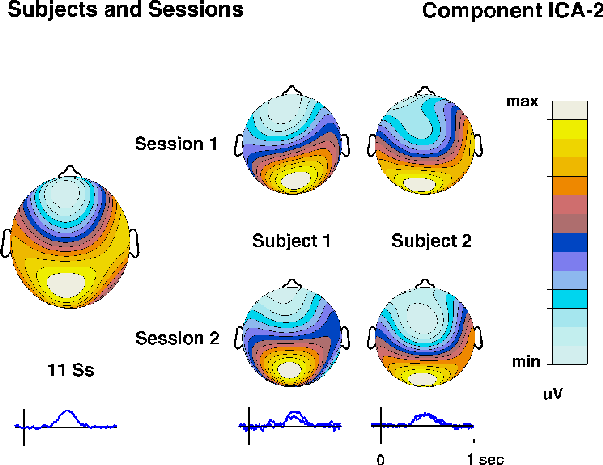
Fig. 3d.
Time courses and topographies of corresponding ICA-2 components
obtained in separate decompositions of detected-target responses
in two separate sessions from two subjects
(right columns)
and from the grand-mean detected-target response for 11 subjects
(left column).
Note the nearly identical time courses
(right traces)
and scalp maps.
The activation waveforms and scalp maps of the ICA components with
largest projected activities were relatively robust to changes in initial weights,
the number of training conditions, and even the number and placement
of electrodes. For example, decomposing the data in Fig. 2a using
arbitrary subsets of 11 of the 14 channels gave components whose
activations and scalp projections correlated 0.9 or above with
ICA components 1, 4, 5, 6, 8, and 9 of Fig. 2b.
ICA decompositions of electric and magnetic
evoked responses to a variety of stimuli from several experiments
(unpublished) proved similar in character and stability.
The algorithm is particularly effective at detecting common response
topography in multiple response conditions, and quantifying differences
between conditions in activation strength of multiple components.
Relation to traditional peak analysis
ERP components usually are identified with individual
event-related response peaks (e.g. N1, P2, N2, etc.) which were
first supposed to represent the activities of brain areas involved in
discrete stages of information processing. However even the peaks of a
response waveform may sum the spatially and temporally overlapping
activities from two or more brain areas with different time courses
of activation {NaatPict87}. When this happens, the scalp
topography of the response appears to move continuously
even when the brain locations
of the active generators are fixed, producing different peak latencies
at each scalp site. This is incompatible with the assumption that each
peak represents a single response component arising in a fixed brain area.
ICA accounts for channels differences in ERP peak latencies by decomposing
the activity under each peak into two or more ICA components,
each having a spatially fixed scalp topography.
Relation to Principal Component Analysis
Another linear transformation method previously proposed for ERP
decomposition {ChapMcC95}, Principal component analysis (PCA),
finds orthogonal directions of greatest variance in the data,
whereas ICA finds nearly temporally-independent (not just uncorrelated)
components whose maps may be non-orthogonal (Fig. 1b). Principal components
of data generated by temporally sparse and independent, but spatially
non-orthogonal sources will be linear combinations of activity
in all the sources, whereas ICA components of the data will individually
identify the larger sources.
The proposed Varimax extension of the PCA method rotates the PCA vectors
to maximize the variance of their activation waveforms {ChapMcC95}.
However, the relevance of this criterion to ERP genesis is unclear.
Applying PCA to the ERP data in Fig. 2a, either alone or followed by
Varimax rotation, produced components active throughout both responses
(unpublished) with minimal correspondence to the ICA components. When evoked
brain activity arises through temporally distinct or partially overlapping
activations of independently-active neural populations, then ICA appears to be
a more appropriate method for separating their contributions to scalp data.
The exploratory use of ICA decomposition for ERP analysis
is based on three assumptions:
(1) that summation at scalp electrodes of potentials
arising in different brain areas is linear; (2) that ERPs are largely
the sum of relatively-brief activations in a restricted set of
spatially-stable brain areas, networks, or neural populations; (3)
that the time-courses of activation are largely temporally-independent.
The first two assumptions appear reasonable.
The third assumption limits the decomposition to temporally independent
components.
To explore the
strengths and limitations of the method, we ran a number of numerical
simulations in which 600-point signals recorded from the cortex of a
patient during preparation for operation for epilepsy were projected
to simulated scalp electrodes
through a three-shell spherical model {Tech-2, Tech-1}.
We used electrocorticographic data in these simulations as a plausible
best approximation to the temporal dynamics of the unknown ERP brain
generators. Results confirmed that the ICA algorithm could accurately
identify the activation waveforms and scalp topographies of relatively
large and more temporally-independent simulated sources,
even in the presence of a large number of small and temporally independent
simulated sources.
However, given simulated ERP activity arising from separate brain
generators whose time courses of activation were made substantially
correlated, the algorithm parsed the resulting
continuously-varying scalp responses into distributed activity within
overlapping subsets of the simulated sources {Tech-2}.
Similarly, SSR components ICA-8 and ICA-9 (Fig. 3c) collected synchronous
bilateral SSR activity instead of splitting it into components
with left- and right-sided topographies, and the neural populations
generating the activities accounted for by two spatially overlapping components,
for example ICA-4 and ICA-5 (Fig. 3b), might not be disjoint since
their scalp distributions are so similar.
More generally, given data summing components
(however defined) that are not temporally independent, spatially fixed,
or sparsely activated, or whose number is not the same as the number
of data channels, the algorithm will not reproduce the original component
distribution, and other linear blind separation algorithms may
produce somewhat different results.
Note that for data sets in which the channel means differ significantly
from the baseline means, removing the channel mean offsets prior to analysis
introduces into the decomposition an implicit DC component without physiological
significance. Methods for dealing with such data sets will be presented
elsewhere.
The range of ERP components that can be separated by the algorithm
is illustrated by the single broad component (ICA-2), accounting for
the posterior P3 response to detected targets as well as the accompanying
anterior negativity (Fig. 3a), and the three near-periodic ICA components
(ICA8, ICA-9, ICA-10) that together accounted for 95.3% of the total SSR (Fig. 3c).
This ICA decomposition of the auditory SSR into three spatially-fixed
components contrasted sharply with a previously proposed interpretation
that spatial SSR instability reflects a moving crest of activity
sweeping through cortex every 25 msec {LR93}.
By itself, however, ICA cannot be used to decide between these
or other source models {Pantev93, ION91}.
ICA decomposition opens a new and potentially useful window into
complex event-related brain data that can complement other analysis
techniques. Further research will be required to fully assess the value
and limitations of temporal independence as a segregation criterion.
Blind separation by ICA decomposition appears
promising for multidimensional measurement of the effects of
experimental variables on electric and magnetic evoked-response
components representing rapid and discrete stages of brain information
processing, particularly when these overlap in scalp distribution. The
method may be especially effective for comparing the activations of
brain response components that are differentially activated in several
related stimulus and cognitive task conditions. Although it may be
difficult to locate ICA components within the brain on the basis of
their time courses and scalp projections, ICA decomposition might
nonetheless prove useful for preprocessing data prior to applying source
localization algorithms. ICA decomposition may be useful as well for
observing event-related changes in the spatial structure of correlated
ongoing EEG activity
in multiple brain areas {Bullock95, Gevins, Lehmann, Rappels, Venky96}.
The method should be equally applicable to magnetoencephalographic
(MEG) data, and can be generalized to track changes in the
spatial structure of EEG or MEG activity in different brain states {MB96}.
Aine, C. J.,
A conceptual overview and critique of functional neuroimaging techniques
in humans: I. MRI/FMRI and PET.
Crit. Rev. Neurobiol. 9, 229-309 (1995).
Snyder, A. Z., Abdullaev, Y. G., Posner, M. I. & Raichle, M. E.,
Scalp electrical potentials reflect regional cerebral blood flow responses during processing of written words.
Proc. Natl. Acad. Sci. USA 92, 1689-1693 (1995).
Makeig, S. & Inlow, M.,
Lapses in alertness: Coherence of fluctuations in performance and EEG spectrum.
Electroencephalogr. clin. Neurophysiol. 86, 23-35 (1993)
Naatanen, R. & Picton, T.,
The N1 wave of the human electric and magnetic response to sound:
a review and an analysis of the component structure.
Psychophysiology 24, 375-425 (1987).
Nunez, P.L.,
Electric Fields of the Brain. New York: Oxford (1981).
Scherg, M. & Von Cramon, D., Evoked dipole source potentials of the human auditory cortex.
Electroencephalogr. Clin. Neurophysiol. 65, 344-601 (1986).
Dale, A.M. & Sereno, M.I.,
Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction - a linear approach.
J. Cogn. Neurosci.
5, 162-176 (1993).
Chapman, R.M. & McCrary, J.W.,
EP component identification and measurement by principal components analysis.
Brain Lang. 27, 288-301 (1995).
Bell, A.J. & Sejnowski, T.J.,
An information-maximization approach to blind separation and blind deconvolution,
Neural Computation 7, 1129-1159 (1995).
Makeig, S., Bell, A.J., Jung, T-P. & Sejnowski T.J.,
Independent component analysis of electroencephalographic data.
Advances in Neural Information Processing Systems
8, 145-151, MIT Press (1996).
Linsker, R., Local synaptic learning rules suffice to maximise mutual information in a linear network.
Neural Computation 4, 691-702 (1992).
Nadal, J-P. & Parga, N.,
Non-linear neurons in the low noise limit: a factorial code maximises information transfer.
Network 5, 565-581 (1994).
Cover, T.M. & Thomas, J.A.,
Elements of Information Theory
John Wiley (1991).
Bell, A.J. & Sejnowski, T.J.,
Learning the higher-order structure of a natural sound,
Network: Computation in Neural Systems 7, 2 (1996).
Cichocki A., Unbehauen R., & Rummert E.,
Robust learning algorithm for blind separation of signals,
Electronics Letters 30, 1386-1387 (1994).
Amari S., Cichocki, A. & Yang, H.H.,
A new learning algorithm for blind signal separation. In:
Advances in Neural Information Processing Systems 8, MIT Press (1996).
Galambos, R., Makeig, S. & Talmachoff P.,
A 40 Hz auditory potential recorded from the human scalp,
Proc. Natl. Acad. Sci. USA 78, 2643-2647 (1981).
Makeig, S., Jung, T-P.,
Ghahremani, D. & Sejnowski, T.J.,
Independent Component Analysis of Simulated ERP Data.
Tech. Rep. INC-9606, Institute for Neural Computation, San Diego, CA. (1996).
Ghahremani, D., Makeig, S., Jung, T-P.,
Bell, A.J. & Sejnowski, T.J.,
Independent Component Analysis of Simulated EEG Using a Three-Shell Spherical Head Model.
Tech. Rep. INC-9601, Institute for Neural Computation, San Diego, CA. (1996).
Bullock, T. H., McClune, M. S., Achimowicz, J. Z., Iragui-Madoz, V. J.,
Duckrow, R. B. & Spencer, S. S., Temporal fluctuations in coherence of brain waves.
Proc. Natl. Acad. Sci. USA 92, 11568-11572 (1995).
Gevins, A.,
High resolution evoked potentials of cognition.
Brain Topography 8, 189-199 (1996).
Wackermann, J,, Lehmann, D., Michel, C. M., & Strik, W. K.,
Adaptive segmentation of spontaneous EEG map series into spatially defined microstates.
Int. J. Psychophysiol. 14, 269-83 (1993).
Rappelsberger, P., Pfurtscheller, G., & Filz, O.,
Calculation of event-related coherence--a new method to study short-lasting coupling between brain areas.
Brain Topography 7, 121-127 (1994).
Bell, A.J. & Sejnowski, T.J.,
Fast blind separation based on information theory.
Proc. Intern. Symp. on Nonlinear Theory and Applications,
Las Vegas (1995).
Comon, P.,
Independent component analysis, a new concept?
Signal Processing 36, 287-314 (1994).
Jutten, C. & Herault, J.,
Blind separation of sources, part I: an adaptive algorithm based on neuromimetic architecture.
Signal Processing
24, 1-10 (1991).
Karhumen, J., Oja, E., Wang, L., Vigario, R. & Joutsenalo, J.,
A class of neural networks for independent component analysis,
IEEE Trans. Neural Networks (to appear).
Cardoso, J-F. & Laheld, B., Equivalent adaptive source separation,
IEEE Trans. Signal Proc. (to appear).
Perrin, F., Pernier, J., Bertrand, O., & Echallier, J.F.,
Spherical splines for scalp potential and current density mapping.
Electroencephalogr. Clin. Neurophysiol.
72, 184-187 (1989).
Pantev, C., Elbert, T., Makeig, S., Hampson, S., Eulitz, C. & Hoke, M.,
Relationship of transient and steady-state auditory evoked fields.
Electroencephalogr. clin. Neurophysiol. 88, 389-396 (1993).
Venkatesh, N. Murthy & Fetz, E.,
Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys
J. Neurophysiol.
76, 3968-3982 (1996).
Olshausen, B.
C.B.C.L. Paper 138, Dept. of Brain and Cognitive Sciences, MIT (1996).
Llinas, R, & Ribary, U.,
Coherent 40-Hz oscillation characterizes dream state in humans.
Proc. Nat. Acad. Sci. USA 90:2078-81 (1993).
Hillyard, S. A. & Munte, T. F.,
Selective attention to color and location:
an analysis with event-related brain potentials.
Percept. Psychophys., 36, 185-98 (1984).
Van Sweden, B., Van Dijk, J. G. & Caekebeke, J. F.,
Auditory information processing in sleep:
late cortical potentials in an oddball paradigm.
Neuropsychobiology, 29:152-6 (1994).
Pearlmutter, B. A. & Parra, L. C.,
A context-sensitive generalization of ICA.
International Conference on Neural Information Processing, Hong Kong (1996).
Ribary, U., Ioannides, A. A., Singh, K. D., Hasson, R., Bolton, J. P., Lado, F., Mogilner, A. & Llinas R.
Magnetic field tomography of coherent thalamocortical
40-Hz oscillations in humans.
Proc. Nat. Acad. Sci. USA
88:11037-11041 (1991).
This report was supported in part by grants to S.M., T-P.J. and T.J.S.
from the Office of Naval Research, and to T.J.S. from the Howard Hughes
Medical Institute.
The authors acknowledge F.S. Elliott and M. Inlow for help in collecting
and processing the data, A. Dale for supplying the head model, and
M. McKeown, S. Hillyard, L. Anllo-Vento, and J. Hansen for discussions and
assistance with graphics.
This report was supported in part by
the Navy Medical Research and Development Command
and the Office of Naval Research, Department of the Navy
under work unit ONR.Reimb-6429.
The views expressed in this article are those of the authors
and do not reflect the official policy or position of the Department
of the Navy, Department of Defense, or the U.S. Government.
Approved for public release, distribution unlimited.
ERP (event-related potential);
EEG (electroencephalgram); SSR (steady-state response); ICA
(independent component analysis); PCA (principal component analysis)
The evoked response data and a
Matlab toolbox for ICA / EEG are available online.
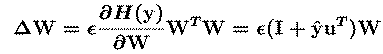
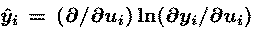
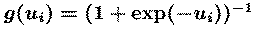
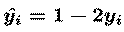
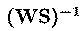
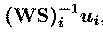
Application to evoked response decomposition
Results
Stability of the decomposition
Nearly identical ICA components were recovered from evoked responses
collected on different days from the same subject, and similar ICA
components from different subjects in the same experiment (Fig. 3d).
Discussion
Conclusions
References
Acknowledgments