This page covers the procedure and results for measuring the latency of the eyetracker designed by Matthew Grivich that is used at SCCN's laboratories. A detailed definition of this system (as well as a name for the device itself) is currently in the works. Incidentally the eye tracking software that Matthew has written (and can be obtained as part of the LSL Apps package found here) is somewhat modular. This makes it very difficult to measure the actual latency.
However it has been shown that a video feed (recorded and LSL timestamped by one of the modes in the eyetracking application GazStream.exe) results in a latency of 28.9ms. (Please see the synchronization report by Matthew concerning this topic for further information on this point.) Yet the collection of camera data is only one part of this eyetracking system.
In order to utilize the system, one must instantiate GazeStream.exe twice. One instance must run in the 'eye camera' mode, the other in the 'scene camera' mode. In the code itself, it is in the 'scene camera' loop that the final answer to the question of where the subject is looking is finally answered. Thus the total latency is the latency of the camera feed plus some other unknown latency -- the time it takes the 'scene camera' algorithm to receive data from the 'eye camera' algorithm and determine the correct eye position.
We hypothesize that there will be a 28.9ms latency from the eye camera to the GazeStream application. We also hypothesize that there is some lag due to the heavy computation necessary to carry out the eye tracker's algorithms. We hypothesize (or rather we hope) that this time is less than the time it takes for the next video frame to come into the system -- that is less than 33.33ms (30Hz).
In order to measure the latency of the system, I first modified the code of the GazeStream software so that it would output extra LSL markers. By doing this I was able to determine when the 'eye camera' (the first stage of computation) first began its loop and when the 'scene camera' (the last stage) finished.
In order to synchronize the streams, a very similar procedure to that outlined here was used. As in that experiment, a photo-transistor (run through a BioSemi amplifier) was used to measure the brightness of a screen whose color oscillates between black and white every second. The scene camera itself was used as a video to synchronize with this signal. Since we record both the timestamps of the eye camera as well as those of the scene camera, we can verify that there is synchrony between the two parts of the eyetracking system.
Furthermore, since we have timestamps for the beginning and end of the entire life cycle of one iteration of the eyetracking system's analyses, we can measure the length of time this computation actually occupies.
The video, BioSemi voltage, and time stamp information was analyzed with this code which depends on first analyzing the video captured by GazeStream.exe in its scene camera mode. This can be done with this code. This depends on the matlab toolbox mmread as well as a plotting function. For more information on this analysis procedure, I refer you again to Matthew's synchronization report
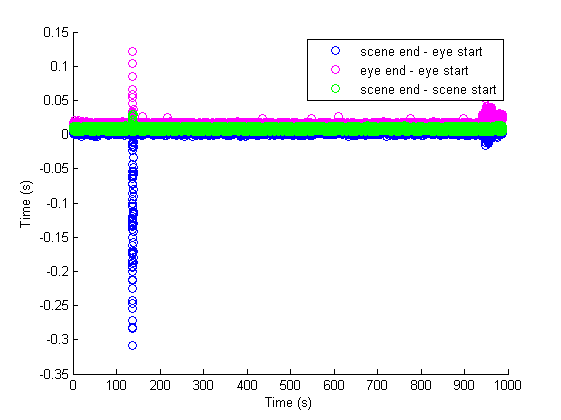
As in that report, this code was used to generate screen flashes. You will need PsychoPhysicsToolbox in your Matlab path if you wish to replicate this experiment.First we verify the latency from the start to the end of the eyetracking computation cycle. We can compute the difference between start and end times of both the eye camera loop as well as the scene camera loop, and (most importantly) the end of the scene camera loop minus the start of the eye camera loop. We see that our hopes are fulfilled and that it indeed takes comfortably less than 33.33ms to crunch a frame of camera data into eye position output.


Furthermore, we see that the median time for this computation is 4.4ms.
We see that we are comfortably within one frame for compute time. We do notice, however, a disconcerting sector of outliers about 120 second into the analysis. This was no doubt caused by some factor stalling the system. The fact that both the scene and eye camera end-start times are affected suggests that this was a delay within the computer doing the eye tracking analysis. Perhaps Acrobat reader needed upgrading at that moment. But the fact that it happened only once in 1000 seconds is encouraging. Below is a closeup. Since it is all done through LSL, it should be the case that when the eye camera loop can't deliver its data on time to the scene camera loop, that the previous sample gets pulled again. This would 'feel' like a slowing of tracking velocity to a subject -- i.e. the marker would be slow to follow the actual gaze.
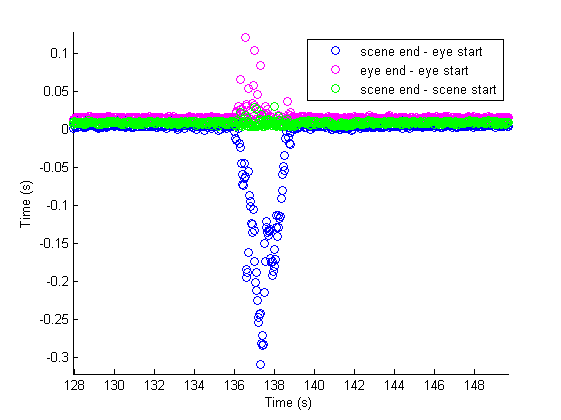
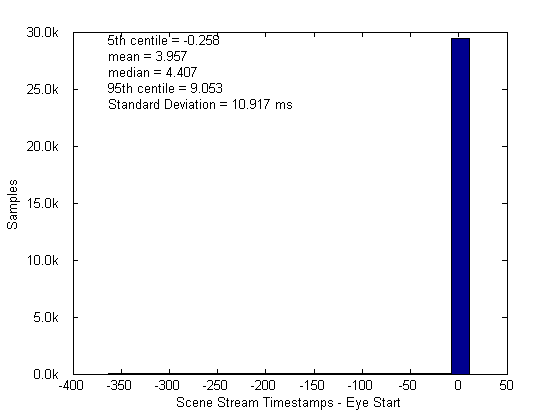
Here comes the punchline. Both cameras and monitors will drop frames. This means that sometimes there will be 59 (or fewer) frames in one second as opposed to 60. Since we don't know when this is going to happen a priori (it's random) we adjust the data to compensate and so that synchrony can be achieved. Again, please see the video synchronization report for a more in depth discussion. In order to be synchronous with what is actually appearing on screen, it is necessary to remove jitter and compensate for dropped frames in the post processing of our video/camera timestamps. This, however, makes it impossible to determine a precise latency for the eyetracker. The reason is that due to round-off error, the 60Hz stream has a sampling period of slightly more than 2 times the sampling period of a 30Hz stream (.016666 rounds up, and .033333 rounds down). Thus, the difference between the scene camera stream timestamps (which correspond to the time an eye position is reported) is locatable only within a +/-5.05ms span about the actual latency.
Below is a histogram of this analysis as well as a closeup of the binned latencies illustrating the dilemma. We may take the total latency then as the camera lag plus the algorithm lag and realize that our accuracy is to within +/-5.05ms. Fortunately the spread of the algorithm lag is within this boundary, so we can ignore it.
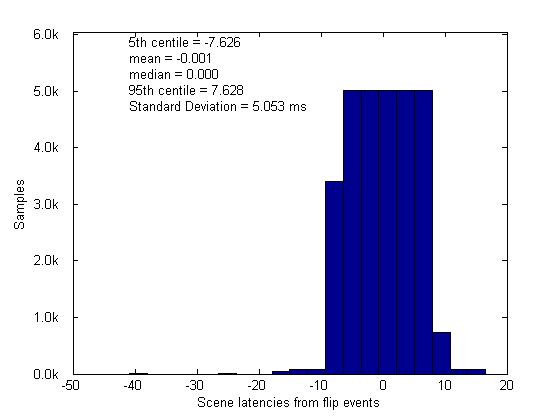
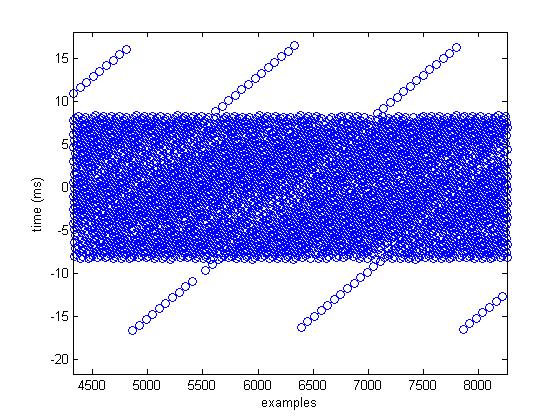
Incidentally, if we don't synchronize the data we can get a much tighter spread with far fewer outliers, i.e. we measure the latency of the algorithm only and the numerical error due to rounding (a direct result of the synchronization process) vanishes. Since we often want to synchronize, however, we resort to this method for our answer.
The other problem is that occasionally, the dropped eye camera and the scene camera will drop frames and (far less occasionally) this will happen during the same analysis period. In these cases the time difference between the moment that the eye camera captures the position of the eye and when the final result is spat out of the scene camera procedure may be as much as one frame's width of video (33.333ms) apart. This temporal distance will also be distorted to some unknown degree due to the post-processing procedure of snapping frame events to a regular frame rate.
In a very bad, worst case situation, it could be the case that there is lag that is more than 33.33ms. It is potentially possible that there could be lags of n times this value since the roundoff error about the flip times wraps around this value. I verified that this is not the case here (and thus presumably not the case in any lab with a reasonably fast computer doing the eyetracking) by looking at the video itself (interpolated to the scene camera stream's timestamps) to verify that the frames are lining up at least within each frame flip.
In this figure we see the BioSemi (remember this is the screen brightness) in blue and the actual camera data (as processed by the functions mentioned above) in magenta. The vertical lines indicate the post-processed flip times of the stimulus in red, the post-processed scene camera events (the times a frame of video is finished processing) are in green, and the time the screen switches from black to white (black). Although the signals are smoothed and normalized, it is clear that the video stream lags behind the BioSemi stream by less than one flip (33.33ms). However, this may not be true on slower systems that use inferior video cards and should be checked by lining up video and voltage signals as illustrated here.
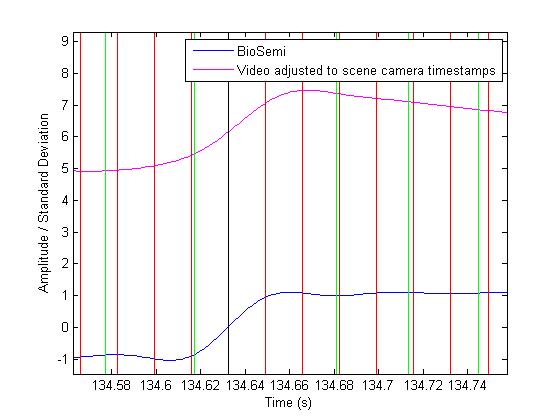
It is unreasonable to expect greater temporal accuracy than that provided by the hardware's sampling period. Thus we conclude that the eye tracking data has a lag of 28.9ms (the camera lag time), but that the actual timing is only accurate within +/- 5.05ms due to the frame rate and the jitter corrections. There is also an average, but variable, lag of 4.4ms for the algorithm to compute, but this lag is obliterated by the synchronization process, which distorts camera stream timestamps beyond this value.
The data for this experiment were gathered on 11/04/2014.